题目内容
2．
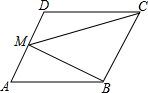如图，M是平行四边形ABCD的一边AD上的任意一点，若△CMB的面积为S，△CDM的面积为S1，△ABM的面积为S2，则下列大小关系正确的为（ ）| A． | S＞S1+S2 | B． | S＜S1+S2 | C． | S=S1+S2 | D． | 无法确定 |
分析 由平行四边形ABCD的面积和△CMB的面积的计算，得出△CMB的面积=$\frac{1}{2}$S平行四边形ABCD，即可得出结论．
解答 解：作MN⊥BC于N；如图所示：
∵S平行四边形ABCD=BC•MN，△CMB的面积=$\frac{1}{2}$BC•MN，
∴△CMB的面积=$\frac{1}{2}$S平行四边形ABCD，
∴△CMB的面积=△CDM的面积+△ABM的面积，
即S=S1+S2；
故选：C．
点评 本题考查了平行四边形的性质、平行四边形的面积、三角形面积的计算；熟练掌握平行四边形的性质，得出平行四边形和三角形之间的面积关系是解决问题的关键．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
13．若2x-1=16，则x等于（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
17．
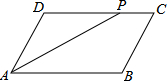如图，平行四边形ABCD中，AB=18cm，PC=6cm，AP是∠DAB的平分线，则平行四边形ABCD的周长为（ ）
如图，平行四边形ABCD中，AB=18cm，PC=6cm，AP是∠DAB的平分线，则平行四边形ABCD的周长为（ ）| A． | 60cm | B． | 48cm | C． | 36cm | D． | 64cm |
11．
已知AB∥CD，点P是AB上方一点，∠1=60°，∠2=35°，则∠3的度数是（ ）
已知AB∥CD，点P是AB上方一点，∠1=60°，∠2=35°，则∠3的度数是（ ）| A． | 30° | B． | 35° | C． | 20° | D． | 25° |
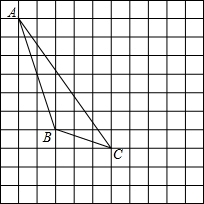如图，每个小正方形的边长为1个单位，每个小方格的顶点叫格点．