题目内容
10. 在一个边长为a的正方形材料上截取一扇形,围成母线长为a的圆锥.
在一个边长为a的正方形材料上截取一扇形,围成母线长为a的圆锥.(1)试设计两种不同的截法(要求每一种截法尽量减少浪费的材料),并把截法在图上表示出来;
(2)分别求出(1)中两种不同的截法所得的圆锥底面的半径和高;
(3)(1)中哪一种截法所得的圆锥侧面积较大?
分析 (1)实际上带有很强的操作性,学生可以实际画画试试,找出方法.
(2)根据不同的截法,计算其所得的圆锥底面的半径和高.
(3)根据不同的截法,计算其圆锥侧面积,比较哪种更好.
解答 解:(1)设计方案示意图如下.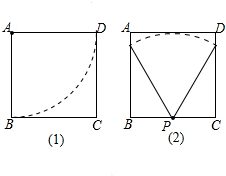
(2)设圆锥底面的半径r,圆锥底面的高h,依题意有:
扇形弧长等于圆锥底面周长,
第一种图弓形的周长为:$\frac{90πa}{180}$=$\frac{πa}{2}$,
∴2πr=$\frac{πa}{2}$,
∴r=$\frac{a}{4}$,
∴h=$\sqrt{{a}^{2}-{r}^{2}}$=$\frac{\sqrt{15}}{4}$a,
第二种图弓形的周长为:$\frac{60πa}{180}$=$\frac{πa}{3}$,
∴2πr=$\frac{πa}{3}$,
∴r=$\frac{a}{6}$,
∴h=$\sqrt{{a}^{2}-{r}^{2}}$=$\frac{\sqrt{35}}{6}$a;
(3)∵①图扇形面积为:$\frac{90π{a}^{2}}{360}$=$\frac{π{a}^{2}}{4}$,
②图扇形面积为:$\frac{60π{a}^{2}}{360}$=$\frac{π{a}^{2}}{6}$,
∴第一种截法所得的圆锥侧面积较大.
点评 本题考查了作图-应用与设计图,正方形的性质,切线的性质,弓形的计算,扇形的计算,勾股定理的应用等.

练习册系列答案
相关题目
2.下列命题中,假命题是( )
| A. | 方差是衡量一组数据波动大小的统计量 | |
| B. | 影响鞋店进货时决策的主要统计量是众数 | |
| C. | 对角线互相垂直且相等的四边形是正方形 | |
| D. | 对角线互相平分的四边形是平行四边形 |
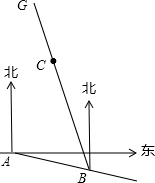 如图所示,某工程队要在一社区点C处修建一条小路CE,使小路CE与AB方向一致.
如图所示,某工程队要在一社区点C处修建一条小路CE,使小路CE与AB方向一致.