题目内容
13.某建筑物的窗户为黄金矩形,已知它较长的一边长为l米,则较短的一边长为$\frac{\sqrt{5}-1}{2}$米.(结果保留根号或者3位小数)分析 设较短的一边长为xm,根据黄金分割的定义得到方程,然后解方程即可.
解答 解:设较短的一边长为xm,根据题意有$\frac{x}{1}$=$\frac{\sqrt{5}-1}{2}$,
解得x=$\frac{\sqrt{5}-1}{2}$,
答:较短的一边长为$\frac{\sqrt{5}-1}{2}$m.
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=$\frac{\sqrt{5}-1}{2}$AB≈0.618AB,并且线段AB的黄金分割点有两个.

练习册系列答案
相关题目
3.已知甲数=2×2×3×5,乙数=2×3×3×5,那么甲数和乙数的最小公倍数是( )
| A. | 60 | B. | 90 | C. | 120 | D. | 180 |
8.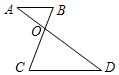 如图,已知AD、BC相交于点O,下列说法错误的是( )
如图,已知AD、BC相交于点O,下列说法错误的是( )
 如图,已知AD、BC相交于点O,下列说法错误的是( )
如图,已知AD、BC相交于点O,下列说法错误的是( )| A. | 若AB∥CD,则∠B=∠C | B. | 若∠A=∠D,则AB∥CD | ||
| C. | 若∠B=∠AOB,则∠DOC=∠C | D. | ∠A+∠B=∠C+∠D |
18.下列各式运算正确的是( )
| A. | a2+a3=a5 | B. | a10÷a2=a5 | C. | (ab2)3=ab6 | D. | a2•a3=a5 |
5.2017年5月18日“北京第9届月季文化节”拉开帷幕,月季花已经成为北京绿化美化的“当家花旦”,月季“花墙”成为了北京城市一道靓丽的风景线.近几十年,园林技术人员一直在开展月季花的培育和驯化研究,其中一些品种的月季花的花朵大小是技术人员关心的问题,技术人员在条件相同的试验环境下,对两个试验田的月季花随机抽取了15朵,并把抽样花朵的直径数据整理记录如下:
表1 甲试验田花朵的直径统计表
表2 乙试验田花朵的直径统计表
回答下列问题:
(1)若将花朵的直径不小于10(单位:cm)的月季花记为优良品种,完成下表:
(2)某次景观布置,需要考虑用到的月季花的花朵直径大小相对均匀,根据以上数据,你认为技术人员应选用哪个试验田的月季花?说明理由.
表1 甲试验田花朵的直径统计表
| 样品 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 花朵的直径 (单位:cm) | 5 | 6 | 7 | 7 | 8 | 8 | 9 | 10 | 11 | 12 | 12 | 13 | 15 | 15 | 17 |
| 样品 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 花朵的直径 (单位:cm) | 7 | 8 | 8 | 9 | 9 | 9 | 9 | 10 | 11 | 11 | 12 | 12 | 12 | 13 | 15 |
(1)若将花朵的直径不小于10(单位:cm)的月季花记为优良品种,完成下表:
| 优良品种数量 | 平均数 | |
| 甲试验田 | 8 | 10.33 |
| 乙试验田 | 8 | 10.33 |
2.下列方程是一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | x2+$\frac{1}{x}$=3 | C. | x2-3x+1=3 | D. | xy=1 |
3.在一个不透明的盒子里装有4个分别写有数字-3、-2、-1、0的小球,它们除数字不同外其余全部相同,现从盒子里随机取出一个小球,记下数字a后放回,再取出一个记下数字b,那么点(a,b)在抛物线y=-x2+1上的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{3}{16}$ | D. | $\frac{1}{4}$ |
 如图,点B,E,C,F在同一条直线上,AB∥DE,∠A=∠D,试判断∠F与∠ACF的数量关系,并说明理由.
如图,点B,E,C,F在同一条直线上,AB∥DE,∠A=∠D,试判断∠F与∠ACF的数量关系,并说明理由.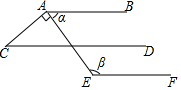 如图,∠α和∠β的度数满足方程组$\left\{\begin{array}{l}{2α+β=230}\\{3α-β=20}\end{array}\right.$.
如图,∠α和∠β的度数满足方程组$\left\{\begin{array}{l}{2α+β=230}\\{3α-β=20}\end{array}\right.$.