题目内容
 如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC.
如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC.(1)求证:∠AEC=90°;
(2)试判断以点A,O,C,D为顶点的四边形的形状,并说明理由;
(3)若DC=2,求DH的长.
考点:切线的性质,等边三角形的判定与性质,菱形的判定与性质,解直角三角形
专题:证明题,几何综合题
分析:(1)连接OC,根据EC与⊙O切点C,则∠OCE=90°,由题意得
=
=
,∠DAC=∠CAB,即可证明AE∥OC,则∠AEC+∠OCE=180°,从而得出∠AEC=90°;
(2)四边形AOCD为菱形.由(1)得
=
,则∠DCA=∠CAB可证明四边形AOCD是平行四边形,再由OA=OC,即可证明平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形);
(3)连接OD.根据四边形AOCD为菱形,得△OAD是等边三角形,则∠AOD=60°,再由DH⊥AB于点F,AB为直径,在Rt△OFD中,根据sin∠AOD=
,求得DH的长.
 |
| AD |
 |
| CD |
 |
| CB |
(2)四边形AOCD为菱形.由(1)得
 |
| AD |
 |
| CB |
(3)连接OD.根据四边形AOCD为菱形,得△OAD是等边三角形,则∠AOD=60°,再由DH⊥AB于点F,AB为直径,在Rt△OFD中,根据sin∠AOD=
| DF |
| OD |
解答:解: (1)连接OC,
(1)连接OC,
∵EC与⊙O切点C,
∴OC⊥EC,
∴∠OCE=90°,
∵点CD是半圆O的三等分点,
∴
=
=
,
∴∠DAC=∠CAB,
∵OA=OC,
∴∠CAB=∠OCA,
∴∠DAC=∠OCA,
∴AE∥OC(内错角相等,两直线平行)
∴∠AEC+∠OCE=180°,
∴∠AEC=90°;
(2)四边形AOCD为菱形.
理由是:
∵
=
,
∴∠DCA=∠CAB,
∴CD∥OA,
又∵AE∥OC,
∴四边形AOCD是平行四边形,
∵OA=OC,
∴平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形);
(3)连接OD.
∵四边形AOCD为菱形,
∴OA=AD=DC=2,
∵OA=OD,
∴OA=OD=AD=2,
∴△OAD是等边三角形,
∴∠AOD=60°,
∵DH⊥AB于点F,AB为直径,
∴DH=2DF,
在Rt△OFD中,sin∠AOD=
,
∴DF=ODsin∠AOD=2sin60°=
,
∴DH=2DF=2
.
 (1)连接OC,
(1)连接OC,∵EC与⊙O切点C,
∴OC⊥EC,
∴∠OCE=90°,
∵点CD是半圆O的三等分点,
∴
 |
| AD |
 |
| CD |
 |
| CB |
∴∠DAC=∠CAB,
∵OA=OC,
∴∠CAB=∠OCA,
∴∠DAC=∠OCA,
∴AE∥OC(内错角相等,两直线平行)
∴∠AEC+∠OCE=180°,
∴∠AEC=90°;
(2)四边形AOCD为菱形.
理由是:
∵
 |
| AD |
 |
| CB |
∴∠DCA=∠CAB,
∴CD∥OA,
又∵AE∥OC,
∴四边形AOCD是平行四边形,
∵OA=OC,
∴平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形);
(3)连接OD.
∵四边形AOCD为菱形,
∴OA=AD=DC=2,
∵OA=OD,
∴OA=OD=AD=2,
∴△OAD是等边三角形,
∴∠AOD=60°,
∵DH⊥AB于点F,AB为直径,
∴DH=2DF,
在Rt△OFD中,sin∠AOD=
| DF |
| OD |
∴DF=ODsin∠AOD=2sin60°=
| 3 |
∴DH=2DF=2
| 3 |
点评:本题考查了切线的性质、等边三角形的判定和性质、菱形的判定和性质以及解直角三角形,是中学阶段的重点内容.

练习册系列答案
相关题目
下列各组根式是同类二次根式的是( )
A、a
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,在四边形ABCD中,∠ACB=90°,AC=BC.过点B作BE∥AD,交CD于点E,在CD上截取DF=CE,如果∠1=∠2.
如图,在四边形ABCD中,∠ACB=90°,AC=BC.过点B作BE∥AD,交CD于点E,在CD上截取DF=CE,如果∠1=∠2.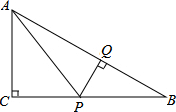 在Rt△ABC中,∠C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足为Q,连接AP.
在Rt△ABC中,∠C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足为Q,连接AP.
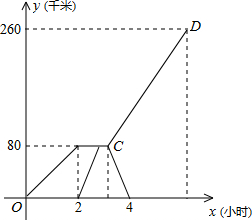 已知,A、B两市相距260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回,同时甲车以原速1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车行驶时间x(小时)之间的函数图象,结合图象回答下列问题:
已知,A、B两市相距260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回,同时甲车以原速1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车行驶时间x(小时)之间的函数图象,结合图象回答下列问题: