题目内容
 如图,小明和小亮玩一种“机器人迈步游戏”,某一个机器人在图中的1号位置上,按顺时针方向,第一次跳一步到2号位置上,第二次跳两步跳到4号位置上,第三次跳三步又跳到了1号位置上,第四次跳四步…一直进行下去,那么如果第2006次跳2006步,所跳到的位置号是( )
如图,小明和小亮玩一种“机器人迈步游戏”,某一个机器人在图中的1号位置上,按顺时针方向,第一次跳一步到2号位置上,第二次跳两步跳到4号位置上,第三次跳三步又跳到了1号位置上,第四次跳四步…一直进行下去,那么如果第2006次跳2006步,所跳到的位置号是( )| A、2 | B、4 | C、5 | D、6 |
考点:规律型:数字的变化类
专题:规律型
分析:先求出2006次跳动所跳动的总步数,然后根据6步为一个循环组,用2006除以6,所得的余数是几就在第几步对应的位置上.
解答:解:∵第一次跳一步,第二次跳两步,第三次跳三步,第四次跳四步…第2006次跳2006步,
∴2006次总共跳:1+2+3+4+…+2006=
=2013021,
2013021÷6=335503…3,
∵三步所对应的位置是4号位置,
∴第2006次跳2006步,所跳到的位置号是4号.
故选B.
∴2006次总共跳:1+2+3+4+…+2006=
| 2006×(2006+1) |
| 2 |
2013021÷6=335503…3,
∵三步所对应的位置是4号位置,
∴第2006次跳2006步,所跳到的位置号是4号.
故选B.
点评:本题是对数字变化规律的考查,读懂题意,求出2006次所跳动的总步数并找出循环规律是解题的关键.

练习册系列答案
相关题目
 有理数a,b,c在数轴上对应的点如图所示,则下面式子中正确的是( )
有理数a,b,c在数轴上对应的点如图所示,则下面式子中正确的是( )| A、c+b>a+b |
| B、ac>ab |
| C、cb<ab |
| D、cb>ab |
若一个凸多边形的边数恰好是从某个顶点引出的对角线的条数的
倍,则这个多边形的内角和是( )
| 4 |
| 3 |
| A、1080° |
| B、1540° |
| C、1800° |
| D、2160° |
甲、乙、丙、丁四名运动员参加4×100米接力赛,如果甲必须安排在第二棒,那么,这四名运动员在比赛中的接棒顺序有( )
| A、4种可能 | B、5种可能 |
| C、6种可能 | D、8种可能 |
如果
是二次根式,则x的取值范围是( )
| 5-x |
| A、x≠5 | B、x=5 |
| C、x≥5 | D、x≤5 |
 如图,点A在x轴正半轴上,OA=2,∠AOB=30°,∠ABO=45°.
如图,点A在x轴正半轴上,OA=2,∠AOB=30°,∠ABO=45°.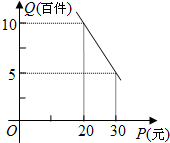 单价P(元)的关系如图所示;维持企业的正常运转每月需最低生活费外的各种开支2000元.
单价P(元)的关系如图所示;维持企业的正常运转每月需最低生活费外的各种开支2000元.