题目内容
9.已知二次函数y=-x2+(k+1)x+3,当x<1时,y随x的增大而增大,当x>1时,y随x的增大而减小.(1)写出这个二次函数的表达式;
(2)这个二次函数有最大值还是最小值?最大(小)值是几?
分析 (1)由增减性可求得其对称轴,则可求得k的值,可求得函数表达式;
(2)把解析式化为顶点式,结合开口方向可求得答案.
解答 解:
(1)∵y=-x2+(k+1)x+3,
∴对称轴为x=-$\frac{k+1}{2×(-1)}$=$\frac{k+1}{2}$,
∵当x<1时,y随x的增大而增大,当x>1时,y随x的增大而减小,
∴对称轴为x=1,
∴$\frac{k+1}{2}$=1,解得k=1,
∴抛物线表达式为y=-x2+2x+3;
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴抛物线开口向下,函数有最大值,最大值为4.
点评 本题主要考查二次函数的性质,掌握抛物线的顶点式是解题的关键,即在y=a(x-h)2+k中,顶点坐标为(h,k),对称轴为x=h.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
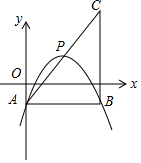 在平面直角坐标系中,已知抛物线y=-$\frac{1}{2}$x2+bx+c(b、c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,-1),点C的坐标为(4,3)直角顶点B在第四象限.
在平面直角坐标系中,已知抛物线y=-$\frac{1}{2}$x2+bx+c(b、c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,-1),点C的坐标为(4,3)直角顶点B在第四象限.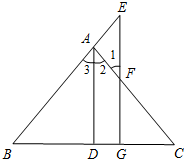 如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠1,求证:∠3=∠2.
如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠1,求证:∠3=∠2. 如图,已知,∠ADC=∠ABC,BE、DF分别平分∠ABC、∠ADC,且∠1=∠2,求证:∠A=∠C.请完成证明过程.
如图,已知,∠ADC=∠ABC,BE、DF分别平分∠ABC、∠ADC,且∠1=∠2,求证:∠A=∠C.请完成证明过程.