题目内容
16.一辆汽车开往距离出发地180千米的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来的1.5倍匀速行驶,并比原计划提前40分钟到达目的地.求前一小时的行驶速度.分析 设前一小时的速度为x千米/时,则一小时后的速度为1.5x千米/时,等量关系为:加速后用的时间+40分钟+1小时=原计划用的时间.注意加速后行驶的路程为180千米-前一小时按原计划行驶的路程.依此列出方程求解即可.
解答 解:设前一小时的速度为x千米/时,则一小时后的速度为1.5x千米/时,
由题意得:1+$\frac{180-x}{1.5x}$+$\frac{2}{3}$=$\frac{180}{x}$,
解得x=60.
经检验:x=60是分式方程的解.
答:前一小时的行驶速度为60千米/时.
点评 本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.

练习册系列答案
相关题目
7.某校组织初三学生电脑技能竞赛,每班选派相同人数去参加竞赛,竞赛成绩分A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分.将初三(1)班和(2)班的成绩整理并绘制成统计图如下.

(1)此次竞赛中(2)班成绩在C级以上(包括C级)的人数为17;
(2)请你将表格补充完整:
(3)试运用所学的统计知识,从两个不同角度评价初三(1)班和初三(2)班的成绩.

(1)此次竞赛中(2)班成绩在C级以上(包括C级)的人数为17;
(2)请你将表格补充完整:
| 平均数(分) | 中位数(分) | 众数(分) | |
| 1班 | 87.5 | 90 | ②90 |
| 2班 | 88 | ①85 | 100 |
5.化简-2a-(1-2a)的值是( )
| A. | -4a-1 | B. | 4a-1 | C. | 1 | D. | -1 |
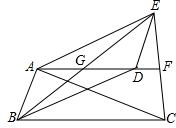 已知△ACE中,AC=AE,AF⊥EC于点F,点D是AF上一点,连接ED,过点A作AB∥DE,过点D作BC∥AE交AB于点B.求证:FG∥BC.
已知△ACE中,AC=AE,AF⊥EC于点F,点D是AF上一点,连接ED,过点A作AB∥DE,过点D作BC∥AE交AB于点B.求证:FG∥BC. 如图,学校课外生物小组的试验园地是边长为20米的正方形,为了便于管理,现要在中间开辟一横一纵共两条等宽的小道,要使种植面积为361平方米,求小道的宽.
如图,学校课外生物小组的试验园地是边长为20米的正方形,为了便于管理,现要在中间开辟一横一纵共两条等宽的小道,要使种植面积为361平方米,求小道的宽.