题目内容
8.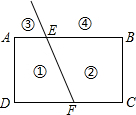 如图,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区城③④位于直线AB上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF的关系(不要求证明).
如图,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区城③④位于直线AB上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF的关系(不要求证明).
分析 先根据矩形的性质得出AB∥CD,再分点P分别位于①、②、③、④四个象限分别求解即可.
解答 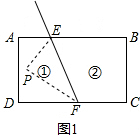 解:如图1,当点P在①区域时,
解:如图1,当点P在①区域时,
∵AB∥CD,
∴∠BEF+∠CFE=180°,
∴∠PEF+∠PFE=(∠PEB+∠PFC)-180°.
∵∠PEF+∠PFE+∠EPF=180°,
∴∠EPF=180°-(∠PEF+∠PFE)=180°-(∠PEB+∠PFC)+180°=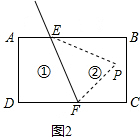 360°-(∠PEB+∠PFC);
360°-(∠PEB+∠PFC);
当点P在区域②时,如图2所示,
∵AB∥CD,
∴∠BEF+∠CFE=180°,
∵∠EPF+∠FEP+∠PFE=180°,
∴∠EPF=∠PEB+∠PFC;
如图3所示,当点P在区域③时,
∵AB∥CD,
∴∠PFC=∠PHB.
∵∠PEH++PEB=180°,
∴∠PEH=180°-∠PEB.
∵∠EPF+∠PEH+∠PHB=180°,即∠EPF+(180°-∠PEB)+∠PFC=180°,
∴∠PEB=∠EPF+∠PFC;
如图4所示,
∵AB∥CD,
∴∠PFC=∠PHB.
∵∠PHB是△PEH的外角,
∴∠PHB=∠EPF+∠PEB,即∠PFC=∠EPF+∠PEB.
点评 本题考查的是平行线的性质,涉及到三角形内角和定理及三角形外角的性质,根据题意作出辅助线,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
19.在计算器上,有很多按键,有的是运算符号键,有的是数字键,按照如图所示的程序进行操作:如表中的x与y分别是输入的6个数及相应的计算结果
上面操作程序中所按的第三个运算符号键和第四个数字键应是+,1.

| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -5 | -2 | 1 | 4 | 7 | 10 |

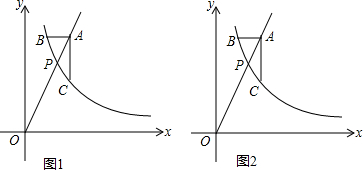
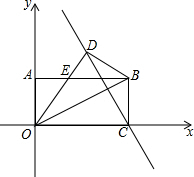 如图,矩形OABC在平面直角坐标系中,OA=2,∠BOC=30°,把△OBC沿OB对折,点C落在点D处,线段OD与AB交于点E.若点P在直线CD上,并且△OEP为直角三角形,求P点坐标.
如图,矩形OABC在平面直角坐标系中,OA=2,∠BOC=30°,把△OBC沿OB对折,点C落在点D处,线段OD与AB交于点E.若点P在直线CD上,并且△OEP为直角三角形,求P点坐标.