题目内容
2.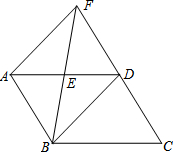 如图,?ABCD中,E为AD的中点,直线BE、CD相交于点F.连接AF、BD.
如图,?ABCD中,E为AD的中点,直线BE、CD相交于点F.连接AF、BD.(1)求证:AB=DF;
(2)若AB=BD,求证:四边形ABDF是菱形.
分析 (1)由平行四边形的性质和已知条件得出∠ABE=∠DFE,AE=DE,由AAS证明△ABE≌△DFE即可证得结论;
(2)由全等三角形的性质得出AB=DF,证出四边形ABDF是平行四边形,再由AB=BD,即可得出结论.
解答 (1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD.
∵点F在CD的延长线上,
∴FD∥AB.
∴∠ABE=∠DFE.
∵E是AD中点,
∴AE=DE.
在△ABE和△DFE中,
$\left\{\begin{array}{l}{∠ABE=∠DFE}\\{∠BEA=∠DEF}\\{AE=DE}\end{array}\right.$,
∴△ABE≌△DFE(AAS)
∴AB=DF;
(2)证明:∵△ABE≌△DFE,
∴AB=DF.
∵AB∥DF,AB=DF,
∴四边形ABDF是平行四边形.
∵AB=BD,
∴四边形ABDF是菱形.
点评 此题考查了平行四边形的性质与判定、全等三角形的判定与性质.此题难度不大,证明三角形全等是解决问题的关键,注意掌握数形结合思想的应用.

练习册系列答案
相关题目

 如图,直线y1=kx+b与双曲线y2=$\frac{m}{x}$交于A,B两点,它们的横坐标分别为1和5.
如图,直线y1=kx+b与双曲线y2=$\frac{m}{x}$交于A,B两点,它们的横坐标分别为1和5.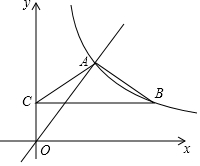 如图,函数y=$\frac{4}{3}$x与函数y=$\frac{m}{x}$(x>0)的图象相交于点A(n,4).点B在函数y=$\frac{m}{x}$(x>0)的图象上,过点B作BC∥x轴,BC与y轴相交于点C,且AB=AC.
如图,函数y=$\frac{4}{3}$x与函数y=$\frac{m}{x}$(x>0)的图象相交于点A(n,4).点B在函数y=$\frac{m}{x}$(x>0)的图象上,过点B作BC∥x轴,BC与y轴相交于点C,且AB=AC.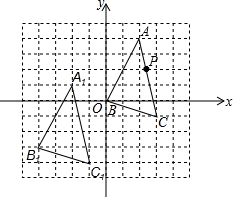 在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为(1.6,1).
在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为(1.6,1).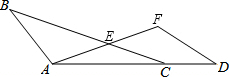 如图,点A,C,D在同一条直线上,BC与AF交于点E,AF=AC,AD=BC,AE=EC.
如图,点A,C,D在同一条直线上,BC与AF交于点E,AF=AC,AD=BC,AE=EC.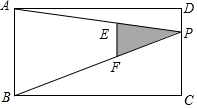 一只小狗在如图所示的矩形草地ABCD内自由的玩耍,点P是矩形的边CD上一点,点E、点F分别为PA,PB的中点,连接EF,则这只小狗跑到△PEF内的概率是$\frac{1}{8}$.
一只小狗在如图所示的矩形草地ABCD内自由的玩耍,点P是矩形的边CD上一点,点E、点F分别为PA,PB的中点,连接EF,则这只小狗跑到△PEF内的概率是$\frac{1}{8}$.