题目内容
8.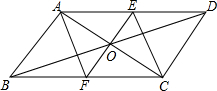 如图:在平行四边形ABCD中,对角线AC与BD交于点O,过点O的直线EF分别与AD、BC交于点E、F,EF⊥AC,连结AF、CE.
如图:在平行四边形ABCD中,对角线AC与BD交于点O,过点O的直线EF分别与AD、BC交于点E、F,EF⊥AC,连结AF、CE.(1)求证:OE=OF;
(2)请判断四边形AECF是什么特殊四边形,请证明你的结论.
分析 (1)首先根据平行四边形的性质可得AD∥BC,OA=CO,再证明△AEO≌△CFO可得OE=OF;
(2)根据△AEO≌△CFO可得AE=CF,然后可得四边形AECF平行四边形,再由条件EF⊥AC可得四边形AECF是菱形.
解答 证明:(1)∵四边形ABCD平行四边形,
∴AD∥BC,OA=CO,
∴∠DAO=∠BCO,
在△AEO和△CFO中$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{AO=CO}\\{∠AOE=∠FOC}\end{array}\right.$,
∴△AEO≌△CFO(ASA),
∴OE=OF;
(2)答:四边形AECF是菱形,
∵△AEO≌△CFO,
∴AE=CF,
∵AE∥FC,
∴四边形AECF平行四边形,
∵EF⊥AC,
∴四边形AECF是菱形.
点评 此题主要考查了全等三角形的判定和性质,以及菱形的判定,关键是掌握对角线互相垂直的平行四边形是菱形.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
9.用科学记数法表示525 000正确的是( )
| A. | 5.25×106 | B. | 5.25×105 | C. | 5.25×104 | D. | 525×103 |
 已知∠MON=40°,P为∠MON内一点,A为OM上的点,B为ON上的点,问当△PAB的周长取最小值时.
已知∠MON=40°,P为∠MON内一点,A为OM上的点,B为ON上的点,问当△PAB的周长取最小值时.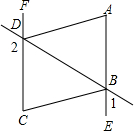 如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.证明:
如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.证明: