题目内容
10.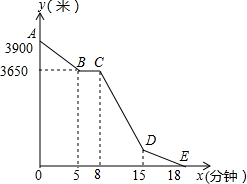 小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.
小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.(1)求小丽步行的速度及学校与公交站台乙之间的距离;
(2)当8≤x≤15时,求y与x之间的函数关系式.
分析 (1)根据函数图象,小丽步行5分钟所走的路程为3900-3650=250米,再根据路程、速度、时间的关系,即可解答;
(2)利用待定系数法求函数解析式,即可解答.
解答 解:(1)根据题意得:
小丽步行的速度为:(3900-3650)÷5=50(米/分钟),
学校与公交站台乙之间的距离为:(18-15)×50=150(米);
(2)当8≤x≤15时,设y=kx+b,
把C(8,3650),D(15,150)代入得:$\left\{\begin{array}{l}{8k+b=3650}\\{15k+b=150}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-500}\\{b=7650}\end{array}\right.$
∴y=-500x+7650(8≤x≤15).
点评 本题考查了一次函数的应用,解决本题的关键是读懂函数图象,获取相关信息,利用得到系数法求函数解析式.

练习册系列答案
相关题目
20.已知∠1=40°,则∠1的余角的度数是( )
| A. | 40° | B. | 50° | C. | 140° | D. | 150° |
1. 如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB为( )
如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB为( )
 如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB为( )
如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB为( )| A. | 70° | B. | 20° | C. | 140° | D. | 35° |
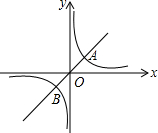 如图,反比例函数y=$\frac{k}{x}$(k>0)与正比例函数y=ax相交于A(1,k),B(-k,-1)两点.
如图,反比例函数y=$\frac{k}{x}$(k>0)与正比例函数y=ax相交于A(1,k),B(-k,-1)两点.
 如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论: 如图,已知点A、P在反比例函数y=$\frac{k}{x}$(k<0)的图象上,点B、Q在直线y=x-3的图象上,点B的纵坐标为-1,AB⊥x轴,且S△OAB=4,若P、Q两点关于y轴对称,设点P的坐标为(m,n).
如图,已知点A、P在反比例函数y=$\frac{k}{x}$(k<0)的图象上,点B、Q在直线y=x-3的图象上,点B的纵坐标为-1,AB⊥x轴,且S△OAB=4,若P、Q两点关于y轴对称,设点P的坐标为(m,n).