题目内容
1. 如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB为( )
如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB为( )| A. | 70° | B. | 20° | C. | 140° | D. | 35° |
分析 由AB是⊙O的直径,根据直径所对的圆周角是直角,可求得∠ACB=90°,继而求得∠B的度数,然后由OB=OC,即可求得答案.
解答 解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=70°,
∴∠B=90°-∠BAC=20°,
∵OB=OC,
∴∠OCB=∠B=20°.
故选B.
点评 此题考查了圆周角定理以及等腰三角形的性质.注意掌握直径所对的圆周角是直角定理的应用.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
13.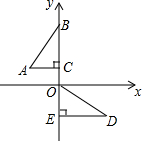 如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
 如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )| A. | △ABC绕点C顺时针旋转90°,再向下平移3 | |
| B. | △ABC绕点C顺时针旋转90°,再向下平移1 | |
| C. | △ABC绕点C逆时针旋转90°,再向下平移1 | |
| D. | △ABC绕点C逆时针旋转90°,再向下平移3 |
11.实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最大的是( )


| A. | a | B. | b | C. | c | D. | d |
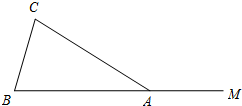 如图,在△ABC中,AB=AC,点M在BA的延长线上.
如图,在△ABC中,AB=AC,点M在BA的延长线上.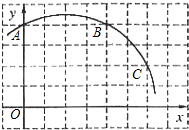 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.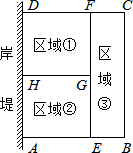 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.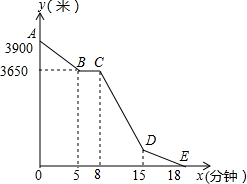 小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.
小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.