题目内容
5.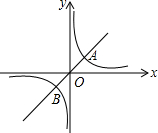 如图,反比例函数y=$\frac{k}{x}$(k>0)与正比例函数y=ax相交于A(1,k),B(-k,-1)两点.
如图,反比例函数y=$\frac{k}{x}$(k>0)与正比例函数y=ax相交于A(1,k),B(-k,-1)两点.(1)求反比例函数和正比例函数的解析式;
(2)将正比例函数y=ax的图象平移,得到一次函数y=ax+b的图象,与函数y=$\frac{k}{x}$(k>0)的图象交于C(x1,y1),D(x2,y2),且|x1-x2|•|y1-y2|=5,求b的值.
分析 (1)首先根据点A与点B关于原点对称,可以求出k的值,将点A分别代入反比例函数与正比例函数的解析式,即可得解.
(2)分别把点(x1,y1)、(x2,y2)代入一次函数y=x+b,再把两式相减,根据|x1-x2|•|y1-y2|=5得出|x1-x2|=|y1-y2|=$\sqrt{5}$,然后通过联立方程求得x1、x2的值,代入即可求得b的值.
解答 解:(1)据题意得:点A(1,k)与点B(-k,-1)关于原点对称,
∴k=1,
∴A(1,1),B(-1,-1),
∴反比例函数和正比例函数的解析式分别为y=$\frac{1}{x}$,y=x;
(2)∵一次函数y=x+b的图象过点(x1,y1)、(x2,y2),
∴$\left\{\begin{array}{l}{{y}_{1}={x}_{1}+b}\\{{y}_{2}={x}_{2}+b}\end{array}\right.$,
②-①得,y2-y1=x2-x1,
∵|x1-x2|•|y1-y2|=5,
∴|x1-x2|=|y1-y2|=$\sqrt{5}$,
由$\left\{\begin{array}{l}{y=x+b}\\{y=\frac{1}{x}}\end{array}\right.$得x2+bx-1=0,
解得,x1=$\frac{-b+\sqrt{{b}^{2}+4}}{2}$,x2=$\frac{-b-\sqrt{{b}^{2}+4}}{2}$,
∴|x1-x2|=|$\frac{-b+\sqrt{{b}^{2}+4}}{2}$-$\frac{-b-\sqrt{{b}^{2}+4}}{2}$|=|$\sqrt{{b}^{2}+4}$|=$\sqrt{5}$,
解得b=±1.
点评 本题考查了反比例函数与正比例函数关于原点对称这一知识点,以及用待定系数法求函数解析式以及一次函数图象上点的坐标特点,利用对称性求出点的坐标是解题的关键.

 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案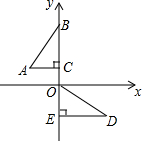 如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )| A. | △ABC绕点C顺时针旋转90°,再向下平移3 | |
| B. | △ABC绕点C顺时针旋转90°,再向下平移1 | |
| C. | △ABC绕点C逆时针旋转90°,再向下平移1 | |
| D. | △ABC绕点C逆时针旋转90°,再向下平移3 |
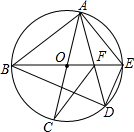 如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )
如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )| A. | △ABE | B. | △ACF | C. | △ABD | D. | △ADE |
 将一张宽为4cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是( )
将一张宽为4cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是( )| A. | $\frac{8}{3}\sqrt{3}$cm2 | B. | 8cm2 | C. | $\frac{16}{3}\sqrt{3}$cm2 | D. | 16cm2 |
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
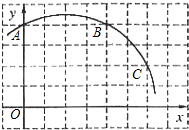 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.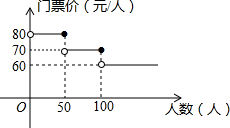 我市某风景区门票价格如图所示,黄冈赤壁旅游公司有甲、乙两个旅游团队,计划在“五一”小黄金周期间到该景点游玩.两团队游客人数之和为120人,乙团队人数不超过50人,设甲团队人数为x人.如果甲、乙两团队分别购买门票,两团队门票款之和为W元.
我市某风景区门票价格如图所示,黄冈赤壁旅游公司有甲、乙两个旅游团队,计划在“五一”小黄金周期间到该景点游玩.两团队游客人数之和为120人,乙团队人数不超过50人,设甲团队人数为x人.如果甲、乙两团队分别购买门票,两团队门票款之和为W元.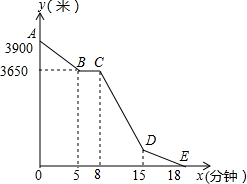 小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.
小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.