Question

6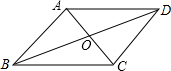．如图，四边形ABCD是菱形，对角线AC、BD相交于点O，且AB=5，BO=4．
（1）求菱形的周长与面积；
（2）求A到CD的距离．

Answer 1

分析 （1）由菱形的四边相等即可求出其周长；利用勾股定理可求出AO的长，再根据菱形的面积公式计算即可求出其面积；
（2）设A到CD的距离为h，根据菱形的面积公式得h×CD=24，进而可求出A到CD的距离．

解答 解：
（1）∵四边形ABCD是菱形，
∴AB=BC=CD=AD=5，AC⊥BD，
∴菱形的周长为4×5=20；
∵AO=$\sqrt{A{B}^{2}-B{O}^{2}}$=3，
∴BD=8，AC=6，
∴菱形面积=$\frac{6×8}{2}$24；
（2）设A到CD的距离为h，根据菱形的面积公式得h×CD=24，
所以h=4.8，
即A到CD的距离为4.8．

点评 本题主要考查利用对角线求面积的方法，求菱形的面积用得较多，需要熟练掌握，能够利用勾股定理求出AO的长是解题关键．