题目内容
17.在Rt△ABC中,∠C=90°,给出下列等式:①BC=AB•sinB;②sinA=tanA•cosA;③sin(90°-∠A)=cosA,其中一定能成立的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 利用锐角三角函数的定义、直角三角形两锐角互余求解即可.
解答 解:①∵∠C=90°,
∴BC=AB•cosB.
故①错误.
②由锐角三角函数的定义可知:sinA=$\frac{a}{c}$,tanA=$\frac{a}{b}$,cosA=$\frac{b}{c}$,
∴sinA=tanA•cosA.
故②正确.
③∵∠B=90°-∠A.
∴sin(90°-∠A)=sinB=cosA.
故③正确.
故选:C.
点评 本题主要考查的是锐角三角函数的定义掌握锐角三角函数的定义是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
7.在平面直角坐标系中,设点A(-8,3)、B(-4,5)及动点C(0,n),D (m,0),当四边形ABCD的周长最小时,C、D的位置的确定方法正确的是( )
| A. | 作点A关于x轴的对称点A′,点B关于y轴的对称点B′,连接A′B′交x轴于点D,交y轴于C | |
| B. | 作点A关于x轴的对称点A′,点B关于y轴的对称点B′,连接A′B′交x轴于点C,交y轴于D | |
| C. | 过A作AD⊥x轴于D点,过B作BC⊥y轴于C点 | |
| D. | 过A作AC⊥x轴于C点,过B作BD⊥y轴于D点 |
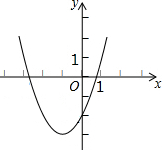 抛物线y=ax2+bx+c的顶点为D(-1,-3),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图所示,则以下结论:①abc>0;②a+b+c<0;③a-c=3;④方程以ax2+bx+c+3=0有两个的实根,其中正确的个数为( )
抛物线y=ax2+bx+c的顶点为D(-1,-3),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图所示,则以下结论:①abc>0;②a+b+c<0;③a-c=3;④方程以ax2+bx+c+3=0有两个的实根,其中正确的个数为( ) 直线m的图象如图所示.试求y与x的函数关系式.小华的解法为:设y=kx.由图象可得2=3k.故k=$\frac{2}{3}$.所以y与x的函数关系式为y=$\frac{2}{3}$x,请你评判小华的做法,如果不正确.请给出正确的作法.
直线m的图象如图所示.试求y与x的函数关系式.小华的解法为:设y=kx.由图象可得2=3k.故k=$\frac{2}{3}$.所以y与x的函数关系式为y=$\frac{2}{3}$x,请你评判小华的做法,如果不正确.请给出正确的作法.