题目内容
15. 如图,从一块直径为4$\sqrt{2}$cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
如图,从一块直径为4$\sqrt{2}$cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )| A. | 2$\sqrt{2}$cm | B. | $\sqrt{2}$cm | C. | 1 cm | D. | 2cm |
分析 先计算出AB,再设这个圆锥的底面圆的半径为r,然后利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长得到2πr=$\frac{90•π•4}{180}$,然后解方程即可.
解答 解:∵直径BC=4$\sqrt{2}$,
∴∠BAC=90°,AB=$\frac{\sqrt{2}}{2}$BC=4,
设这个圆锥的底面圆的半径为r,
根据题意得2πr=$\frac{90•π•4}{180}$,
解得r=1.
故选C.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
5.下列实数中最小的是( )
| A. | -4 | B. | -1 | C. | 0 | D. | $\sqrt{2}$ |
6.下列计算中正确的是( )
| A. | a3•a2=a6 | B. | 2a•a=2a2 | C. | (2a2)2=2a4 | D. | 6a8÷3a2=2a4 |
3.计算(-x2y)3的结果是( )
| A. | -x5y3 | B. | -x6y | C. | x6y3 | D. | -x6y3 |
20.下列成语中描述的事件是随机事件的是( )
| A. | 水中捞月 | B. | 瓮中捉鳖 | C. | 拔苗助长 | D. | 守株待兔 |
7.已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)的对应值如下表所示:
则方程ax2+bx+2=0的根是( )
| … | 0 | 50 | 200 | … | |
| y | … | 1 | -1 | 1 | … |
| A. | x1=x2=100 | B. | x1=0,x2=200 | C. | x1=50,x2=150 | D. | x1=50,x2=250 |
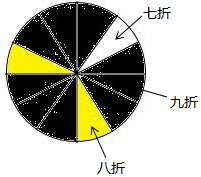 某商场为了吸引顾客,开展了一种转动转盘打折促销的话动,顾客在该商场同一日消费300-1000元时,就可获得一次转动转盘的机会,当转盘停止转动时,指针指向几折(指针落在分界线上时,重新转动一次),顾客就按几折价格付款,消费在1000元以上时,顾客可获得二次转动转盘的机会,顾客可按折上折付款.
某商场为了吸引顾客,开展了一种转动转盘打折促销的话动,顾客在该商场同一日消费300-1000元时,就可获得一次转动转盘的机会,当转盘停止转动时,指针指向几折(指针落在分界线上时,重新转动一次),顾客就按几折价格付款,消费在1000元以上时,顾客可获得二次转动转盘的机会,顾客可按折上折付款.