题目内容
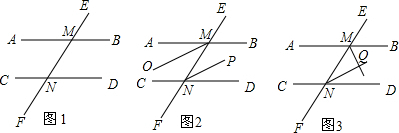
（1）如图1，直线AB，CD被直线EF所截，且AB∥CD，根据 可得∠AMN=∠DNM；根据
可得∠BMN+∠DNM= °
（2）如图2，直线AB，CD被直线EF所截，且AB∥CD，MO，NP分别是∠AMN，∠DNM的角平分线，则判断MO与NP的位置关系 ．
（3）如图3，直线AB，CD被直线EF所截，且AB∥CD，MQ，NQ分别是∠BMN，∠DNM的角平分线，则判断MQ与NQ的位置关系 ．
（4）对于上面第（2）、（3）两题，请选择其中一题写出结论成立的推导过程．
可得∠BMN+∠DNM=
（2）如图2，直线AB，CD被直线EF所截，且AB∥CD，MO，NP分别是∠AMN，∠DNM的角平分线，则判断MO与NP的位置关系
（3）如图3，直线AB，CD被直线EF所截，且AB∥CD，MQ，NQ分别是∠BMN，∠DNM的角平分线，则判断MQ与NQ的位置关系
（4）对于上面第（2）、（3）两题，请选择其中一题写出结论成立的推导过程．
考点：平行线的性质
专题：
分析：（1）、（2）、（3）根据平行线的判定与性质以及角平分线的性质进行填空；
（4）如图2，利用根据平行线的性质判定∠AMN=∠DNM．则由角平分线的性质推知∠OMN=∠MNP，故MO∥NP；
如图3，根据平行线的性质得到∠BMN+∠DNM=180°，所以由平行线的性质得到∠QMN+∠QNM=90°，故MQ⊥NQ．
（4）如图2，利用根据平行线的性质判定∠AMN=∠DNM．则由角平分线的性质推知∠OMN=∠MNP，故MO∥NP；
如图3，根据平行线的性质得到∠BMN+∠DNM=180°，所以由平行线的性质得到∠QMN+∠QNM=90°，故MQ⊥NQ．
解答：解：（1）如图1，直线AB，CD被直线EF所截，且AB∥CD，根据 两直线平行，内错角相等可得∠AMN=∠DNM；
根据 两直线平行，同旁内角互补
可得∠BMN+∠DNM=180°；
（2）如图2，直线AB，CD被直线EF所截，且AB∥CD，MO，NP分别是∠AMN，∠DNM的角平分线，则判断MO与NP的位置关系 平行（或MO∥NP）；
（3）如图3，直线AB，CD被直线EF所截，且AB∥CD，MQ，NQ分别是∠BMN，∠DNM的角平分线，则判断MQ与NQ的位置关系 垂直（或MQ⊥NQ）．
（4）（2）的结论的证明：
如图2，∵AB∥CD，
∴∠AMN=∠DNM．
又 MO，NP分别是∠AMN，∠DNM的角平分线，
∴∠OMN=∠MNP，
∴MO∥NP；
（3）结论的证明：
如图3，∵AB∥CD，
∴∠BMN+∠DNM=180°，
又 MQ，NQ分别是∠BMN，∠DNM的角平分线，
∴∠QMN+∠QNM=90°，
∴MQ⊥NQ；
故答案是：（1）两直线平行，内错角相等；两直线平行，同旁内角互补； 180°；
（2）平行（或MO∥NP）；
（3）垂直（或MQ⊥NQ）．
解：（1）如图1，直线AB，CD被直线EF所截，且AB∥CD，根据 两直线平行，内错角相等可得∠AMN=∠DNM；根据 两直线平行，同旁内角互补
可得∠BMN+∠DNM=180°；
（2）如图2，直线AB，CD被直线EF所截，且AB∥CD，MO，NP分别是∠AMN，∠DNM的角平分线，则判断MO与NP的位置关系 平行（或MO∥NP）；
（3）如图3，直线AB，CD被直线EF所截，且AB∥CD，MQ，NQ分别是∠BMN，∠DNM的角平分线，则判断MQ与NQ的位置关系 垂直（或MQ⊥NQ）．
（4）（2）的结论的证明：
如图2，∵AB∥CD，
∴∠AMN=∠DNM．
又 MO，NP分别是∠AMN，∠DNM的角平分线，
∴∠OMN=∠MNP，
∴MO∥NP；
（3）结论的证明：
如图3，∵AB∥CD，
∴∠BMN+∠DNM=180°，
又 MQ，NQ分别是∠BMN，∠DNM的角平分线，
∴∠QMN+∠QNM=90°，
∴MQ⊥NQ；
故答案是：（1）两直线平行，内错角相等；两直线平行，同旁内角互补； 180°；
（2）平行（或MO∥NP）；
（3）垂直（或MQ⊥NQ）．
点评：本题利用了平行线的性质：两直线平行，内错角相等；两直线平行，同旁内角互补．
练习册系列答案
相关题目
