Question

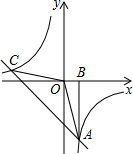如图，已知正比例函数y=kx的图象与反比例函数y=

15-k

x

的图象相交于A、B两点，且A点的横坐标为2．
（1）求A、B两点的坐标；
（2）在x轴上取关于原点对称的P、Q两点（P点在Q点的右边），试问：四边形AQBP一定是一个什么形状的四边形？并说明理由；
（3）上述四边形AQBP能否为矩形？若能，请求出点P、Q的坐标和矩形AQBP的面积；
若不能，请说明理由．

Answer 1

考点：反比例函数综合题

专题：

分析：（1）设A点坐标为（2，t），把A（2，t）分别代入y=kx和y=

15-k

x

可求出k=3，t=6，则A点坐标为（2，6），再根据正比例函数图象和反比例函数图象的性质得到点A与点B关于原点对称，所以B点坐标为（-2，-6）；
（2）如图，由点A与点B关于原点对称得到OA=OB，由点P与点Q关于原点对称得到OP=OQ，则根据平行四边形的判定方法即可判断四边形AQBP为平行四边形；
（3）当AB=PQ时，即OA=OP=OQ，平行四边形APBQ为矩形，利用两点间的距离公式计算出OA=2

10

，OP=OQ=2

10

，则可得到P点坐标为（2

10

，0），Q点坐标为（-2

10

，0），然后根据三角形面积公式和矩形的面积=2S_△APQ进行计算．

解答：解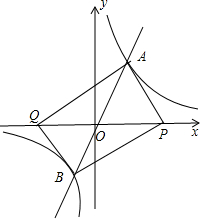：（1）设A点坐标为（2，t），
把A（2，t）分别代入y=kx和y=

15-k

x

得

t=2k t= 15-k 2

，
解得

k=3 t=6

，
所以A点坐标为（2，6），
因为正比例函数y=3x的图象与反比例函数y=

12

x

的图象相交于A、B两点，则点A与点B关于原点对称，
所以B点坐标为（-2，-6）；
（2）如图，四边形AQBP一定是一个平行四边形．理由如下：
因为点A与点B关于原点对称，
所以OA=OB，
又因为点P与点Q关于原点对称，
所以OP=OQ，
所以四边形AQBP为平行四边形；
（3）四边形AQBP能为矩形．
当AB=PQ时，即OA=OP=OQ，平行四边形APBQ为矩形，
因为OA=

22+62

=2

10

，
所以OP=2

10

，
所以P点坐标为（2

10

，0），Q点坐标为（-2

10

，0），
所以矩形的面积=2S_△APQ=2×

1

2

×4

10

×6=24

10

．

点评：本题考查了反比例函数的综合题：熟练掌握反比例函数和正比例函数图象的性质、平行四边形和矩形的判定方法；会运用原点对称的性质和两点间的距离公式．