题目内容
15．已知x为奇数，且$\sqrt{\frac{x-6}{9-x}}$=$\frac{\sqrt{x-6}}{\sqrt{9-x}}$，求$\sqrt{1+2x+{x}^{2}}$的算术平方根．分析 根据二次根式、分式有意义的条件、奇数的定义求出x、y的值，根据算术平方根的概念求解即可．
解答 解：∵$\sqrt{\frac{x-6}{9-x}}$=$\frac{\sqrt{x-6}}{\sqrt{9-x}}$，
∴x-6≥0且9-x＞0，
解得6≤x＜9，
∵x为奇数，
∴x=7，
∴$\sqrt{1+2x+{x}^{2}}$=$\sqrt{1+14+49}$=8，8的算术平方根是2$\sqrt{2}$．
点评 本题考查的是二次根式、分式有意义的条件，分式有意义，分母不为0；二次根式的被开方数是非负数．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
图中∠1+∠2+∠3+∠4+∠5+∠6=360度．
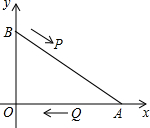如图，在直角坐标系中，已知点A（8，0）、B（0，6），点P由点B出发沿BA方向向点A作匀速直线运动，速度为每秒3个单位长度，点Q由A出发沿AO（O为坐标原点）方向向点O作匀速直线运动，速度为每秒2个单位长度，连接PQ，若设运动时间为t（0＜t＜$\frac{10}{3}$）秒．解答如下问题：
一个几何体，是由许多规格相同的小正方体堆积而成的，某主视图、俯视图如图所示，要摆成这样的图形至少需用6块正方体，最多需用7块正方体．
学校要围一个矩形花圃，其一边利用足够长的墙，另三边用篱笆围成，由于园艺需要，还要用一段篱笆将花圃分隔为两个小矩形部分（如图所示），总共36米的篱笆恰好用完（不考虑损耗）．设矩形垂直于墙面的一边AB的长为x米（要求AB＜AD），矩形花圃ABCD的面积为S平方米．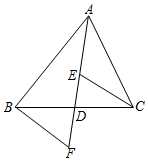
如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE=DF，