题目内容
5．
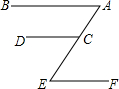如图，AB∥EF，∠ECD=∠E，求证：CD∥AB．
分析 由AB∥EF可得到∠A=∠E，结合条件可得∠A=∠DCE，由同位角相等，两直线平行，可判定AB∥CD．
解答 证明：
∵AB∥EF，
∴∠A=∠E，
又∠DCE=∠E，
∴∠DCE=∠A，
∴AB∥CD．
点评 本题主要考查平行线的判定和性质，掌握平行线的性质和判定是解题的关键，即①同位角相等?两直线平行，②内错角相等?两直线平行，③同旁内角互补?两直线平行，④a∥b，b∥c⇒a∥c．
练习册系列答案
相关题目
15．
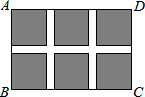如图，某小区规划在一个长30m、宽20m的长方形土地ABCD上修建三条同样宽的通道，使其中两条与AB平行，另一条与AD平行，其余部分钟花草，要使每一块花草的面积都为78cm2，那么通道宽应设计成多少m？设通道宽为xm，则由题意列得方程为（ ）
如图，某小区规划在一个长30m、宽20m的长方形土地ABCD上修建三条同样宽的通道，使其中两条与AB平行，另一条与AD平行，其余部分钟花草，要使每一块花草的面积都为78cm2，那么通道宽应设计成多少m？设通道宽为xm，则由题意列得方程为（ ）| A． | （30-x）（20-x）=78 | B． | （30-2x）（20-2x）=78 | C． | （30-2x）（20-x）=6×78 | D． | （30-2x）（20-2x）=6×78 |
13．下列分式中，无论x取什么值，总有意义的是（ ）
| A． | $\frac{1}{{x}^{2}+1}$ | B． | $\frac{x}{2x+1}$ | C． | $\frac{1}{{x}^{2}}$ | D． | $\frac{x-5}{x}$ |
20．若代数式$\frac{{\sqrt{x+5}}}{x-1}$有意义，则x应满足（ ）
| A． | x=0 | B． | x≠1 | C． | x≥-5 | D． | x≥-5且x≠1 |
如图，由几个相同的小正方体搭成的一个几何体，它的俯视图为（ ）
