题目内容
19.下列计算正确的是( )| A. | x2+x4=x6 | B. | x3÷x2=x | C. | (x2)3=x5 | D. | (2x2)3=2x6 |
分析 根据合并同类项法则,同底数幂相除,底数不变指数相减;幂的乘方,底数不变指数相乘;积的乘方,先把积的每一个因式分别乘方,再把所得的幂相乘对各选项分析判断即可得解.
解答 解:A、x2与x4不是同类项,不能相加,故本选项错误;
B、x3÷x2=x3-2=x,故本选项正确;
C、(x2)3=x2×3=x6,故本选项错误;
D、(2x2)3=23•x2×3=8x6,故本选项错误.
故选B.
点评 本题考查合并同类项、同底数幂的除法、幂的乘方、积的乘方,熟练掌握运算性质和法则是解题的关键.

练习册系列答案
相关题目
11.下面图形都是由同样大小的平行四边形按一定的规律组成,其中,第①个图形一共有1个平行四边形,第②个图形一共有5个平行四边形,第③个图形一共有11个平行四边形,…,则第⑥个图形中平行四边形的个数为( )
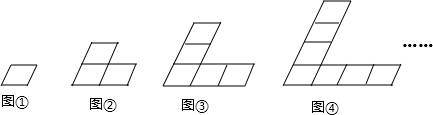

| A. | 45 | B. | 35 | C. | 41 | D. | 65 |
7.要使代数式$\frac{x}{\sqrt{x-3}}$有意义,则x的取值范围是( )
| A. | x=3 | B. | x>3 | C. | x≥3 | D. | x≠0 |
11.计算(2ab)2的结果是( )
| A. | 2ab2 | B. | 2a2b2 | C. | 4a2b2 | D. | 4ab2 |
8.若$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$是方程kx+3y=1的解,则k等于( )
| A. | -$\frac{5}{3}$ | B. | -4 | C. | $\frac{7}{3}$ | D. | $\frac{1}{4}$ |