题目内容
16.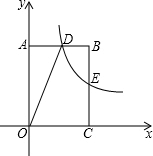 如图,双曲线y=$\frac{k}{x}$(k≠0)经过矩形OABC的边AB的中点D,交BC于点E.若梯形ODBC的面积为6,则双曲线的解析式为y=$\frac{4}{x}$.
如图,双曲线y=$\frac{k}{x}$(k≠0)经过矩形OABC的边AB的中点D,交BC于点E.若梯形ODBC的面积为6,则双曲线的解析式为y=$\frac{4}{x}$.
分析 先根据矩形的特点设出B、C的坐标,根据矩形的面积求出B点横纵坐标的积,由D为AB的中点求出D点的横纵坐标,再由待定系数法即可求出反比例函数的解析式.
解答 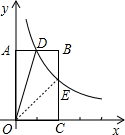 解:连接OE,
解:连接OE,
设此反比例函数的解析式为y=$\frac{k}{x}$(k≠0),C(c,0),
则B(c,b),E(c,$\frac{b}{2}$),
设D(x,y),
∵D和E都在反比例函数图象上,
∴xy=k,$\frac{bc}{2}$=k,
即S△AOD=S△OEC=$\frac{1}{2}$×c×$\frac{b}{2}$,
∵梯形ODBC的面积为6,
∴bc-$\frac{1}{2}$×c×$\frac{b}{2}$=6,
∴$\frac{3}{4}$bc=6,
∴bc=8,
∴S△AOD=S△OEC=2,
∵k>0,
∴$\frac{1}{2}$k=2,解得k=4,
故答案为:4.
点评 此题考查了反比例函数中比例系数k的几何意义,涉及到矩形的性质及用待定系数法求反比例函数的解析式,难度适中.

练习册系列答案
相关题目
5.若-4x2y和-2xmyn是同类项,则m,n的值分别是( )
| A. | m=2,n=1 | B. | m=2,n=0 | C. | m=4,n=1 | D. | m=4,n=0 |
6.如果$\sqrt{x+2}$=2,那么x等于( )
| A. | 16 | B. | 8 | C. | 4 | D. | 2 |

