题目内容
2. 如图,在△DAE中,∠DAE=30°,线段AE,AD的中垂线分别交直线DE于B,C两点,求∠BAC的度数.
如图,在△DAE中,∠DAE=30°,线段AE,AD的中垂线分别交直线DE于B,C两点,求∠BAC的度数.
分析 由已知条件,利用了中垂线的性质得到线段相等及角相等,再结合三角形内角和定理求解.
解答 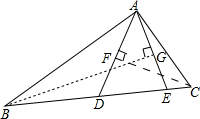 解:如图,∵BG是AE的中垂线,CF是AD的中垂线,
解:如图,∵BG是AE的中垂线,CF是AD的中垂线,
∴AB=BE,AC=CD
∴∠AED=∠BAE=∠BAD+∠DAE,∠CDA=∠CAD=∠DAE+∠CAE,
∵∠DAE+∠ADE+∠AED=180°
∴∠BAD+∠DAE+∠DAE+∠CAE+∠DAE=3∠DAE+∠BAD+∠EAC=90°+∠BAD+∠EAC=180°
∴∠BAD+∠EAC=90°
∴∠BAC=∠BAD+∠EAC+∠DAE=90°+30°=120°.
点评 本题考查了中垂线的性质、三角形内角和定理及等腰三角形的判定与性质;找着各角的关系利用内角和列式求解是正确解答本题的关键.

练习册系列答案
相关题目
12.($\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2014}+\sqrt{2013}}$)•($\sqrt{2014}$+1)=( )
| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |
13.若等腰直角三角形的内切圆半径的长为1,则其外接圆半径的长为( )
| A. | $\sqrt{3}+1$ | B. | $\sqrt{2}+1$ | C. | $\sqrt{2}$ | D. | $\sqrt{2}-1$ |

 已知有理数a,b对应的点在数轴上的位置如图所示,化简:|a-b|-2|a+1|-|b+1|.
已知有理数a,b对应的点在数轴上的位置如图所示,化简:|a-b|-2|a+1|-|b+1|. 如图,直线y=kx+b(k<0,b>0)与双曲线y=$\frac{n}{x}$(n>0,x>0)相交于C、D,分别与x轴、y轴相交于B、A.猜想:AC与DB的数量关系为AC=DB,并加以证明.
如图,直线y=kx+b(k<0,b>0)与双曲线y=$\frac{n}{x}$(n>0,x>0)相交于C、D,分别与x轴、y轴相交于B、A.猜想:AC与DB的数量关系为AC=DB,并加以证明.