题目内容
18．在△ABC中，三条边长分别为a、b、c，以下条件不能证明△ABC是直角三角形的是（ ）| A． | a2=b2+c2 | B． | ∠A+∠B=90° | ||
| C． | △ABC与直角三角形CDE全等 | D． | （a+b）2=c2 |
分析 根据直角三角形的判定逐个判断即可．
解答 解：A、是直角三角形，故本选项不符合题意；
B、∵∠A+∠B=90°，
∴∠C=180°-∠A-∠B=90°，
∴△ABC是直角三角形，故本选项不符合题意；
C、∵△ABC和直角三角形CDE全等，
∴△ABC是直角三角形，故本选项不符合题意；
D、根据（a+b）2=c2不能推出△ABC是直角三角形，故本选项符合题意；
故选D．
点评 本题考查了勾股定理的逆定理和直角三角形的判定，能熟记勾股定理的逆定理的内容是解此题的关键，注意：如果两边的平方和等于第三边的平方，那么这个三角形是直角三角形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．
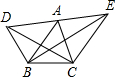如图，已知A是DE的中点，设△DBC，△ABC，△EBC的面积分别为S1，S2，S3，则S1，S2，S3的关系为（ ）
如图，已知A是DE的中点，设△DBC，△ABC，△EBC的面积分别为S1，S2，S3，则S1，S2，S3的关系为（ ）| A． | ${S_2}=\frac{3}{2}（{S_1}+{S_3}）$ | B． | ${S_2}=\frac{1}{2}（{S_3}-{S_1}）$ | C． | ${S_2}=\frac{1}{2}（{S_1}+{S_3}）$ | D． | ${S_2}=\frac{3}{2}（{S_3}-{S_1}）$ |
6．
反比例函数y=$\frac{k}{x}$的图象如图所示，则k的值可能是（ ）
反比例函数y=$\frac{k}{x}$的图象如图所示，则k的值可能是（ ）| A． | -1 | B． | $\frac{3}{2}$ | C． | 3 | D． | 4 |
如图，直角三角尺的直角顶点在直线b上，∠3=25°，转动直线a，当∠1=65°时，a∥b．
如图，有一个边长为4cm的正方形和一个长为8cm、宽为4cm的长方形拼接成一个大长方形，现制作一个与大长方形面积相等的正方形，则这个大正方形的边长是多少？（结果保留小数点后两位）