题目内容
1．
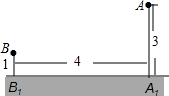如图，大江的一侧有A、B两个工厂，它们有垂直于江边的小路，长度分别为3千米和1千米，设两条小路相距4千米，现在要在江边建立一个抽水站，把水送到A、B两厂去，欲使供水管路最短，抽水站应建在哪里？
分析 延长BB1至点B′，使BB1=B1B′，连接B′A交A1B1于点P，再由△APA1∽△AB′A′即可得出A1P的长，再由勾股定理求出A1P的长即可．
解答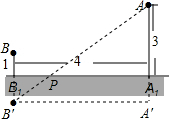 
解：如图所示，
延长BB1至点B′，使BB1=B1B′，连接B′A交A1B1于点P，
∵A1B1=4千米，A1B1∥A′B′，
∴△APA1∽△AB′A′，
∴$\frac{{A}_{1}P}{A′B}$=$\frac{{AA}_{1}}{AA′}$，即$\frac{{A}_{1}P}{4}$=$\frac{3}{4}$，解得A1P=3（千米）．
答：抽水站应建在距A13千米处．
点评 本题考查的是轴对称，最短路线问题，熟知两点之间，线段最短是解答此题的关键．
练习册系列答案
相关题目
11．
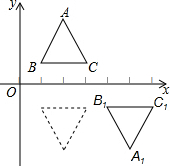在平面直角坐标系中，把△ABC先沿x轴翻折，再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换．如图，已知等边三角形ABC的顶点B、C的坐标分别是（1，1）、（3，1），把三角形经过连续5次这种变换得到三角形△A5B5C5，则点A的对应点A5的坐标是（ ）
在平面直角坐标系中，把△ABC先沿x轴翻折，再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换．如图，已知等边三角形ABC的顶点B、C的坐标分别是（1，1）、（3，1），把三角形经过连续5次这种变换得到三角形△A5B5C5，则点A的对应点A5的坐标是（ ）| A． | （5，-$\sqrt{3}$） | B． | （14，1+$\sqrt{3}$） | C． | （17，-1-$\sqrt{3}$） | D． | （20，1+$\sqrt{3}$） |
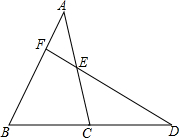在△ABC中，点D在BC的延长线上，E是AC边中点，DE的延长线交AB于点F．
如图，平面上有A、B、C、D4个点，根据下列语句画图．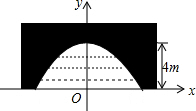
如图是一座古拱桥的截面图，拱桥洞是抛物线形状，其跨度为10m，桥洞与水面的最大距离为4m，将拱桥的横截面放在如图所示的平面直角坐标系中．
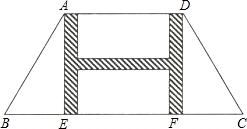如图，有一块等腰梯形的草坪，草坪上底AD长48m，下底BC长108m，上下底之间的距离AE（或DF）是40m．现要在草坪中修建横、纵向的“H”型甬道，甬道宽度相等，设甬道的宽为x m．