题目内容
9. 如图,两个大小相同的球恰好放在一个圆柱形的盒子里,这个圆柱形盒子的剩余容积仅为原来的$\frac{1}{3}$(填几分之几).
如图,两个大小相同的球恰好放在一个圆柱形的盒子里,这个圆柱形盒子的剩余容积仅为原来的$\frac{1}{3}$(填几分之几).
分析 根据圆柱体的体积和球的体积的计算公式即可得到结果.
解答 解:设球的半径为r,
根据题意得:两个球的体积之和=2×$\frac{4}{3}$πr3=$\frac{8}{3}$πr3,
圆柱体盒子容积=πr2•4r=4πr3,
$\frac{\frac{8}{3}π{r}^{3}}{4π{r}^{3}}$=$\frac{2}{3}$,
这个圆柱形盒子的剩余容积仅为原来的1-$\frac{2}{3}$=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题考查了圆柱体的体积,球的体积的计算,整式的混合运算,熟记圆柱体的体积和球的体积的计算公式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.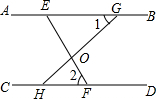 如图所示,AB∥CD,EF、HG相交于点O,∠1=40°,∠2=60°,则∠EOH的角度为( )
如图所示,AB∥CD,EF、HG相交于点O,∠1=40°,∠2=60°,则∠EOH的角度为( )
 如图所示,AB∥CD,EF、HG相交于点O,∠1=40°,∠2=60°,则∠EOH的角度为( )
如图所示,AB∥CD,EF、HG相交于点O,∠1=40°,∠2=60°,则∠EOH的角度为( )| A. | 80° | B. | 100° | C. | 140° | D. | 120° |
17.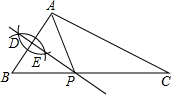 如图,已知△ABC中,AC<BC,分别以点A、点B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点D、点E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是( )
如图,已知△ABC中,AC<BC,分别以点A、点B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点D、点E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是( )
 如图,已知△ABC中,AC<BC,分别以点A、点B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点D、点E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是( )
如图,已知△ABC中,AC<BC,分别以点A、点B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点D、点E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是( )| A. | PA+PC=BC | B. | PA=PB | C. | DE⊥AB | D. | PA=PC |
14.下列说法正确的个数有( )
(1)两条直线被第三条直线所截,内错角相等
(2)如果∠1+∠2+∠3=180°,那么∠1、∠2、∠3互补
(3)对顶角相等
(4)如果两个角的两边分别平行,那么这两个角相等
(5)点到直线的垂线段叫做点到直线的距离.
(1)两条直线被第三条直线所截,内错角相等
(2)如果∠1+∠2+∠3=180°,那么∠1、∠2、∠3互补
(3)对顶角相等
(4)如果两个角的两边分别平行,那么这两个角相等
(5)点到直线的垂线段叫做点到直线的距离.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
1.下列图形中既是轴对称又是中心对称的图形是( )
| A. |  | B. |  | C. |  | D. |  |
19.如果关于x的方程mx2+mx+1=0有两个相等的实数根,那么m等于( )
| A. | 4或0 | B. | $\frac{1}{4}$ | C. | 4 | D. | ±4 |
 由六个完全相同的正方体组成的几何体如图所示.这个几何体的主视图是( )
由六个完全相同的正方体组成的几何体如图所示.这个几何体的主视图是( )