题目内容
4.如图1,在平面直角坐标系中,点O为坐标原点,抛物线y=-x2+bx+a与x轴相交于点A、点B(点A在点B的左侧),与y轴正半轴相较于点C,直线y=kx-3k经过点B、C两点,且△BOC为等腰直角三角形.(1)求抛物线的解析式;
(2)如图2,过点C作直线l∥x轴,P为直线l上方抛物线上一点,连接PB,PB与直线l相交于点D,将线段BD绕点B逆时针旋转90°后得到线段BE,过点E作BC的平行线,它与直线l相交于点F,连接PF,设点P的横坐标为t,△PDF的面积为S,求S与t之间的函数关系式,并直接写出自变量t的取值范围;
(3)如图3,在(2)的条件下,N为PB中点,Q为线段DF上一点,连接PC、QB、QN,当△PCF的面积与△BCD的面积相等,且QN平分∠BQD时,求点Q的坐标.
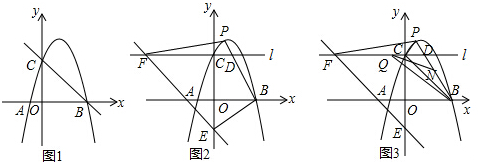
分析 (1)如图1,只需令y=0,即可得到点B的坐标,再根据条件可得到点C的坐标,然后运用待定系数法就可解决问题;
(2)过点B作BG⊥l于G,过点P作PH⊥x轴于H,交DF于K,如图2,易证△BGD≌△BOE,则有DG=OE,∠EOB=∠DGB=90°,即可得到点E在y轴上,然后只需运用割补法就可解决问题;
(3)设PH与BC相交于点R,过点N分别向OB、QB作垂线,垂足分别为W、S,过点Q作AB的垂线,垂足为点J,直线NW与l相交于点Z.连接NR,如图3,由△PCF的面积与△BCD的面积相等可得到S=S△PCB,从而求出PR(用t表示),然后根据PH=PR+RH求出t,从而可得到点P的坐标,设CQ=m,则BJ=OB+OJ=3+m,在△BQJ中,∠BJQ=90°,QJ=OC=3,BJ=3+m,只需表示出BQ(用m表示),然后运用勾股定理就可解决问题.
解答 解:(1)如图1,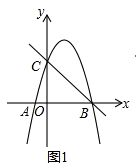
令y=0,得kx-3k=0,
∵k≠0,
∴x=3,B(3,0).
∵△BOC是等腰直角三角形,∠BOC=90°,
∴OB=OC=3,
∴C(0,3).
∵y=-x2+bx+a经过点B、C,
∴$\left\{\begin{array}{l}{-{3}^{2}+3b+a=0}\\{a=3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=3}\\{b=2}\end{array}\right.$,
∴抛物线的解析式为y=-x2+2x+3;
(2)过点B作BG⊥l于G,过点P作PH⊥x轴于H,交DF于K,如图2,
∵直线l∥x轴,
∴PK⊥DF,∠GCO=180°-∠COB=90°,
∴∠CGB=∠GCO=∠COB=90°,
∴四边形COBG是矩形,
∴BG=OC=3=OB,∠GBO=90°.
∵∠GBO=∠PBE=90°,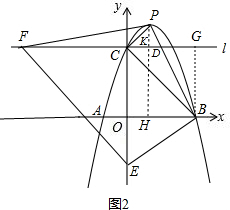
∴∠DBG=∠OBE.
在△BGD和△BOE中,
$\left\{\begin{array}{l}{BD=BE}\\{∠DBG=∠OBE}\\{BG=BO}\end{array}\right.$
∴△BGD≌△BOE,
∴DG=OE,∠EOB=∠DGB═90°,
∴点E在y轴上.
设DG=OE=k,
∵BC∥EF,
∴∠CFE=∠FEC=∠BCO=45°,
∴CF=CE=3+k,
∴DF=CF+CG-DG=3+k+3-k=6,
∴PH=-t2+2t+3.
∵四边形OCKH为矩形,
∴OC=KH=3,
∴PK=PH-KH=-t2+2t.
∴S△PDF=$\frac{1}{2}$DF×PK=-3t2+6t,(0<t<2);
(3)设PH与BC相交于点R,过点N分别向OB、QB作垂线,垂足分别为W、S,
过点Q作AB的垂线,垂足为点J,直线NW与l相交于点Z.连接NR,如图3, S=S△PCF+S△PCD=S△BCD+S△PCD=S△PCB
S=S△PCF+S△PCD=S△BCD+S△PCD=S△PCB
=S△PCR+S△PBR
=$\frac{1}{2}$PR×CK+$\frac{1}{2}$PR×BH
=$\frac{1}{2}$PR(CK+BH)=$\frac{1}{2}$PR(OH+BH)=$\frac{1}{2}$PR×OB,
∴-3t2+6t=$\frac{1}{2}$×3PR,
∴PR=-2t2+4t.
在△BHR中,
∵∠HRB=180°-45°-90°=45°,
∴BH=HR=3-t.
∵PH=PR+RH,
∴-t2+2t+3=-2t2+4t+3-t,
解得:t1=1,t2=0(舍去),
∴P点坐标为(1,4).
可知RH=2=NW,四边形RHWN为矩形,∠NRH=90°.
设CQ=m,则BJ=OB+OJ=OB+QC=3+m.
∵∠BWN=∠BHP=∠PRN=90°,
∴PH∥NW,
∴∠BNW=∠NPR.
在△PNR与△BNW中,
$\left\{\begin{array}{l}{∠PRN=∠NMB}\\{∠RPN=∠WNB}\\{PN=NB}\end{array}\right.$
∴△PRN≌△NWB,
∴BW=NR=HW=$\frac{1}{2}$BH=1,
∴OW=OH+HW=2,
∴CZ=OW=NW=2.
在△NQS与△NQZ中,
$\left\{\begin{array}{l}{∠NSQ=∠NZQ=90°}\\{∠NQS=∠NQZ}\\{QN=QN}\end{array}\right.$
∴△NSQ≌△NZQ,
∴QZ=2+m=SQ,SN=NZ=1=BW.
在Rt△BNW和Rt△NBS中,
$\left\{\begin{array}{l}{SN=BW}\\{BN=NB}\end{array}\right.$
∴Rt△BNW≌Rt△NBS(HL),
∴BS=NW=2,BQ=m+2+2=m+4.
在△BQJ中,
又∵∠BJQ=90°,QJ=OC=3,BJ=3+m,
∴32+(m+3)2=(m+4)2,
解得:m=1,
∴点Q的坐标为(-1,3).
点评 本题主要考查了运用待定系数法求抛物线的解析式,直线上点的坐标特征、全等三角形的判定与性质、等腰三角形的判定与性质、勾股定理等知识,综合性比较强,难度比较大,证到点E在y轴上是解决第(2)小题的关键,把问题归结到Rt△BQJ中并运用勾股定理,是解决第(3)小题的关键.

 智能训练练测考系列答案
智能训练练测考系列答案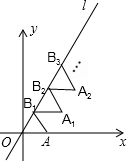 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2016的坐标是(1008,1008$\sqrt{3}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2016的坐标是(1008,1008$\sqrt{3}$).



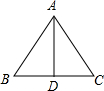 如图,等边△ABC中,AD为高,若AB=6,则CD的长度为3.
如图,等边△ABC中,AD为高,若AB=6,则CD的长度为3. 如图,两个大小相同的球恰好放在一个圆柱形的盒子里,这个圆柱形盒子的剩余容积仅为原来的$\frac{1}{3}$(填几分之几).
如图,两个大小相同的球恰好放在一个圆柱形的盒子里,这个圆柱形盒子的剩余容积仅为原来的$\frac{1}{3}$(填几分之几).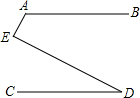 如图所示,若AB∥CD,则∠A,∠D,∠E的度数之间的等量关系是∠A+∠E-∠D=180°.
如图所示,若AB∥CD,则∠A,∠D,∠E的度数之间的等量关系是∠A+∠E-∠D=180°.