题目内容
19.如果关于x的方程mx2+mx+1=0有两个相等的实数根,那么m等于( )| A. | 4或0 | B. | $\frac{1}{4}$ | C. | 4 | D. | ±4 |
分析 若一元二次方程有两不等根,则根的判别式△=b2-4ac=0,建立关于m的方程,求出m的取值,同时还要考虑二次项的系数不能为0.
解答 解:∵关于x的方程mx2+mx+1=0有两个相等的实数根,
∴△=b2-4ac=0,即m2-4×m×1=0,
解得:m=0或m=4,
又∵二次项的系数不能为0,
∴m=4,
故选:C.
点评 本题主要考查一元二次方程的定义及根的判别式,一元二次方程根的情况与判别式△的关系:①△>0?方程有两个不相等的实数根;②△=0?方程有两个相等的实数根;③△<0?方程没有实数根.且注意一元二次方程的二次项系数不为0.

练习册系列答案
相关题目
4.在下列各式中,二次根式$\sqrt{a-1}$的有理化因式是( )
| A. | $\sqrt{a+1}$ | B. | $\sqrt{a-1}$ | C. | $\sqrt{a}+1$ | D. | $\sqrt{a}-1$ |
 如图,两个大小相同的球恰好放在一个圆柱形的盒子里,这个圆柱形盒子的剩余容积仅为原来的$\frac{1}{3}$(填几分之几).
如图,两个大小相同的球恰好放在一个圆柱形的盒子里,这个圆柱形盒子的剩余容积仅为原来的$\frac{1}{3}$(填几分之几).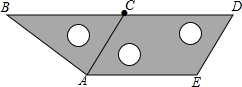 如图,将三个相同的三角板不重叠不留空隙地拼在一起,观察图形,在线段AB,BD,DE,EC,CA,AE中,相互平行的线段有( )
如图,将三个相同的三角板不重叠不留空隙地拼在一起,观察图形,在线段AB,BD,DE,EC,CA,AE中,相互平行的线段有( ) 如图,AB是半圆的直径,点C、D是半圆上两点,∠ADC=128°,则∠ABC=52°.
如图,AB是半圆的直径,点C、D是半圆上两点,∠ADC=128°,则∠ABC=52°.