题目内容
10.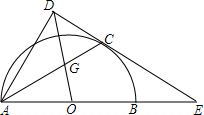 如图,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的直线CD,垂足为D,AB的延长线交直线CD于点E,连接OD交AC于点G,AC平分∠DAB.
如图,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的直线CD,垂足为D,AB的延长线交直线CD于点E,连接OD交AC于点G,AC平分∠DAB.(1)求证:CD是⊙O的切线;
(2)若$\frac{CG}{GA}$=$\frac{3}{4}$,求$\frac{OE}{AE}$的值.
分析 (1)连结OC,根据角平分线的性质得到∠DAC=∠CAB,根据等腰三角形的性质得到∠CAB=∠ACO,等量代换得到∠DAC=∠ACO,推出AD∥OC,根据平行线的性质得到OC⊥DE,即可得到结论;
(2)由于OC∥AD,推出△OCG∽△DAG,根据相似三角形的性质得到$\frac{OC}{DA}$=$\frac{CG}{AG}$=$\frac{3}{4}$,由于OC∥AD,推出△ECO∽△EDA,根据相似三角形的性质即可得到结论.
解答 (1)证明:连结OC,如图,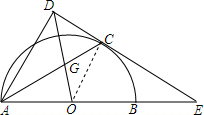 ∵AC平分∠DAB,
∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵OA=OC,
∴∠CAB=∠ACO,
∴∠DAC=∠ACO,
∴AD∥OC,
∵AD⊥DE,
∴OC⊥DE,
∴CD是⊙O的切线;
(2)解:∵OC∥AD,
∴△OCG∽△DAG,
∴$\frac{OC}{DA}$=$\frac{CG}{AG}$=$\frac{3}{4}$,
∵OC∥AD,
∴△ECO∽△EDA,
∴$\frac{OE}{AE}$=$\frac{OC}{AD}$=$\frac{3}{4}$.
点评 本题考查了切线的判定,相似三角形的判定和性质,等腰三角形的性质,平行线的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
18.四边形ABCD中,AB=3,CD=5,M、N分别是边AD,BC的中点,则线段MN的长的取值范围是( )
| A. | 2<MN≤8 | B. | 2≤MN<8 | C. | 1<MN≤4 | D. | 1≤MN<4 |
 ,那么它的实际车牌号是9689.
,那么它的实际车牌号是9689.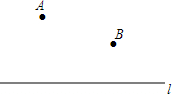 如图,点A,B为直线l外的两点,点P是直线l上的动点,当点P运动到何处时,PA与线段PB之差达到最大?请你在图上标出符合条件的点P的位置.
如图,点A,B为直线l外的两点,点P是直线l上的动点,当点P运动到何处时,PA与线段PB之差达到最大?请你在图上标出符合条件的点P的位置.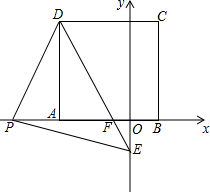 如图,在直角坐标系中,点A(-3,0)和点B(1,0)以AB为边在x轴上方作正方形ABCD,点P是x轴负半轴上一点,连接DP,过点P作DP的垂线与y轴负半轴交于点E,PD=PE,连接DE.
如图,在直角坐标系中,点A(-3,0)和点B(1,0)以AB为边在x轴上方作正方形ABCD,点P是x轴负半轴上一点,连接DP,过点P作DP的垂线与y轴负半轴交于点E,PD=PE,连接DE.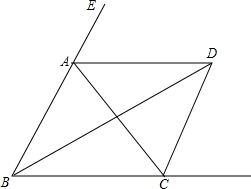 如图所示,在△ABC中,AB=AC,∠EAC和∠FCA均是△ABC的外角,BD平分∠ABC,AD平分∠EAC,CD平分∠ACF,现有以下结论:①AD∥BC;②∠ADC+∠ABD=90°;③∠BDC=$\frac{1}{2}$∠BAC,其中正确的结论有①②③.
如图所示,在△ABC中,AB=AC,∠EAC和∠FCA均是△ABC的外角,BD平分∠ABC,AD平分∠EAC,CD平分∠ACF,现有以下结论:①AD∥BC;②∠ADC+∠ABD=90°;③∠BDC=$\frac{1}{2}$∠BAC,其中正确的结论有①②③.