题目内容
18.四边形ABCD中,AB=3,CD=5,M、N分别是边AD,BC的中点,则线段MN的长的取值范围是( )| A. | 2<MN≤8 | B. | 2≤MN<8 | C. | 1<MN≤4 | D. | 1≤MN<4 |
分析 利用中位线定理可得MG=$\frac{1}{2}$AB=$\frac{3}{2}$,NG=$\frac{1}{2}$CD=$\frac{5}{2}$,由三角形的三边关系得出1<MN<4,再由当MN=MG+NG,即MN=4时,四边形ABCD是梯形,即可得出MN的取值范围.
解答 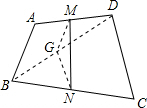 解:连接BD,过M作MG∥AB交BD于G,连接NG.如图所示:
解:连接BD,过M作MG∥AB交BD于G,连接NG.如图所示:
∵M是边AD的中点,AB=3,MG∥AB,
∴MG是△ABD的中位线,
∴BG=GD,MG=$\frac{1}{2}$AB=$\frac{3}{2}$;
∵N是BC的中点,BG=GD,CD=5,
∴NG是△BCD的中位线,
∴NG=$\frac{1}{2}$CD=$\frac{5}{2}$,
在△MNG中,由三角形三边关系可知NG-MG<MN<MG+NG,
即$\frac{5}{2}$-$\frac{3}{2}$<MN<$\frac{5}{2}$+$\frac{3}{2}$,
∴1<MN<4,
当MN=MG+NG,即MN=4时,四边形ABCD是梯形,
故线段MN长的取值范围是1<MN≤4.
故选:C.
点评 本题考查了三角形中位线定理、三角形的三边关系;解答此题的关键是根据题意作出辅助线,利用三角形中位线定理及三角形三边关系解答.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
7.若a=-0.22,b=-2-2,c=(-$\frac{1}{2}$)-2,d=(-$\frac{1}{2}$)0,则a,b,c,d的大小关系为( )
| A. | a>b>c>d | B. | c>d>a>b | C. | c>d>b>a | D. | d>a>b>c |
 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).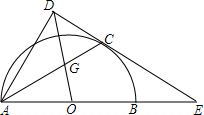 如图,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的直线CD,垂足为D,AB的延长线交直线CD于点E,连接OD交AC于点G,AC平分∠DAB.
如图,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的直线CD,垂足为D,AB的延长线交直线CD于点E,连接OD交AC于点G,AC平分∠DAB.