题目内容
13. 已知:二次函数y1=x2+bx+c的图象经过A(-1,0),B(0,-3)两点.
已知:二次函数y1=x2+bx+c的图象经过A(-1,0),B(0,-3)两点.(1)求y1的表达式及抛物线的顶点坐标;
(2)点C(4,m)在抛物线上,直线y2=kx+b(k≠0)经过A,C两点,当y1>y2时,求自变量x的取值范围;
(3)将直线AC沿y轴上下平移,当平移后的直线与抛物线只有一个公共点时,求平移后直线的表达式.
分析 (1)把A(-1,0)、B(0,-3)两点代入y1得求出b和c的值即可;
(2)根据图象即可得到当y1>y2时,求自变量x的取值范围;
(3)设直线AC平移后的表达式为y=x+k,使x2-2x-3=x+k,根据△=0,求出k的值即可.
解答 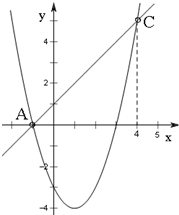 解:(1)把A(-1,0)、B(0,-3)两点代入y1得
解:(1)把A(-1,0)、B(0,-3)两点代入y1得
$\left\{\begin{array}{l}{1-b+c=0}\\{c=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$
即y1=x2-2x-3,
顶点坐标(1,-4),
(2)把C(4,m)代入y1,
m=5,所以C(4,5),
把A、C两点代入y2得:y2=x+1,
如图所示:x的取值范围:x<-1或x>4,
(3)设直线AC平移后的表达式为y=x+k
得:x2-2x-3=x+k,
令△=0,
解得k=-$\frac{21}{4}$,
所以平移后直线的表达式:y=x-$\frac{21}{4}$.
点评 本题主要考查了二次函数图象与几何变换、待定系数法求二次函数的解析式,以及二次函数与不等式的知识,解题的关键是正确求出一次函数和二次函数的解析式,此题难度不大.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
12.下列各式中,运算结果是9m2-16n2的是( )
| A. | (3m+2n)(3m-8n) | B. | (-4n+3m)(-4n-3m) | C. | (-3m+4n)(-3m-4n) | D. | (4n+3m)(4n-3m) |
5. 下列四个图案中,能通过如图图案平移得到的是( )
下列四个图案中,能通过如图图案平移得到的是( )
 下列四个图案中,能通过如图图案平移得到的是( )
下列四个图案中,能通过如图图案平移得到的是( )| A. |  | B. |  | C. |  | D. |  |
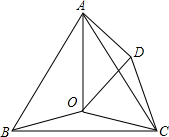 已知:如图,O是等边△ABC内一点,∠AOB=105°,将△BOC绕点C顺时针旋转使CB与CA重合,得到△ADC,连接OD.
已知:如图,O是等边△ABC内一点,∠AOB=105°,将△BOC绕点C顺时针旋转使CB与CA重合,得到△ADC,连接OD.
 已知△ABC中,AB=AC,∠BAC=45°,绕点C顺时针旋转△ABC,使点B落在AB边上,得△A1B1C(如图),联结AA1
已知△ABC中,AB=AC,∠BAC=45°,绕点C顺时针旋转△ABC,使点B落在AB边上,得△A1B1C(如图),联结AA1

 如图1,三角形ABC的各顶点均在格点上,将三角形ABC平移得到三角形A1,B1,C1,使A1点的坐标为(-1,4),
如图1,三角形ABC的各顶点均在格点上,将三角形ABC平移得到三角形A1,B1,C1,使A1点的坐标为(-1,4),