题目内容
19.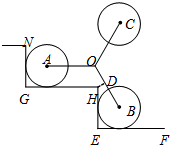 如图是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图,定长的轮架杆OA,OB,OC抽象为线段,有OA=OB=OC,且∠AOB=120°,折线NG-GH-HE-EF表示楼梯,CH,EF是水平线,NG,HE是铅垂线,半径相等的小轮子⊙A,⊙B与楼梯两边相切,且AO∥GH.
如图是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图,定长的轮架杆OA,OB,OC抽象为线段,有OA=OB=OC,且∠AOB=120°,折线NG-GH-HE-EF表示楼梯,CH,EF是水平线,NG,HE是铅垂线,半径相等的小轮子⊙A,⊙B与楼梯两边相切,且AO∥GH.(1)如图①,若点H在线段OB上,则$\frac{BH}{OH}$的值是$\sqrt{3}$.
(2)如果一级楼梯的高度$HE=({8\sqrt{3}+2})cm$,点H到线段OB的距离d满足条件d≤3cm,那么小轮子半径r的取值范围是(11-3$\sqrt{3}$)cm≤r≤8cm.
分析 (1)如图①,P为⊙B的切点,连接BP并延长,作OL⊥BP于点L,交GH于点M,求出ML,OM,根据$\frac{BH}{OH}$=$\frac{ML}{OM}$求解;
(2)如图②,作HD⊥OB,P为切点,连接BP,PH的延长线交BD延长线于点L,由△LDH∽△LPB,得出$\frac{DL}{PL}$=$\frac{DH}{PB}$,再根据30°的直角三角形得出线段的关系,得到DH和r的关系式,根据0≤d≤3的限制条件,列不等式组求范围.
解答  解:(1)如图①,P为⊙B的切点,连接BP并延长,作OL⊥BP于点L,交GH于点M,
解:(1)如图①,P为⊙B的切点,连接BP并延长,作OL⊥BP于点L,交GH于点M,
∴∠BPH=∠BLO=90°,
∵AO∥GH,
∴BL∥AO∥GH,
∵∠AOB=120°,
∴∠OBL=60°,
在RT△BPH中,HP=$\sqrt{3}$BP=$\sqrt{3}$r,
∴ML=HP=$\sqrt{3}$r,
OM=r,
∵BL∥GH,
∴$\frac{BH}{OH}$=$\frac{ML}{OM}$=$\frac{\sqrt{3}r}{r}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$. (2)如图②,作HD⊥OB,P为切点,连接BP,PH的延长线交BD延长线于点L,
(2)如图②,作HD⊥OB,P为切点,连接BP,PH的延长线交BD延长线于点L,
∴∠LDH=∠LPB=90°,
∴△LDH∽△LPB,
∴$\frac{DL}{PL}$=$\frac{DH}{PB}$,
∵AO∥PB,∠AOD=120°,
∴∠B=60°,
∴∠BLP=30°,
∴DL=$\sqrt{3}$DH,LH=2DH,
∵HE=(8$\sqrt{3}$+2)cm
∴HP=8$\sqrt{3}$+2-r,
PL=HP+LH=8$\sqrt{3}$+2-r+2DH,
∴$\frac{\sqrt{3}DH}{2DH+8\sqrt{3}+2-r}$=$\frac{DH}{r}$,解得DH=$\frac{\sqrt{3}+1}{2}$r-4$\sqrt{3}$-1,
∵0cm≤DH≤3cm,
∴0≤$\frac{\sqrt{3}+1}{2}$r-4$\sqrt{3}$-1≤3,
解得:(11-3$\sqrt{3}$)cm≤r≤8cm.
故答案为:(11-3$\sqrt{3}$)cm≤r≤8cm.
点评 本题主要考查了圆的综合应用,解决本题的关键是作出辅助线,运用含30°的直角三角形的性质得出线段的关系,同时涉及切线的性质,平行线分线段成比例的性质的知识点,综合性较强,难度较大.

 阅读快车系列答案
阅读快车系列答案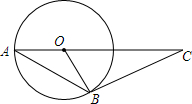 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=25°,则∠C的度数是( )
如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=25°,则∠C的度数是( )| A. | 65° | B. | 50° | C. | 40° | D. | 25° |
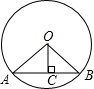 如图,AB是⊙O的弦,OC⊥AB,垂足为C,若OA=5,OC=4,则AB的长为6.
如图,AB是⊙O的弦,OC⊥AB,垂足为C,若OA=5,OC=4,则AB的长为6. 一只蜘蛛正处于一个正方体的一个顶点A处,一只苍蝇处于此正方体的另一个顶点B处(如图所示),如果此正方体的棱长恰为10cm,试问蜘蛛想捉到苍蝇的最短路线是10$\sqrt{5}$cm.
一只蜘蛛正处于一个正方体的一个顶点A处,一只苍蝇处于此正方体的另一个顶点B处(如图所示),如果此正方体的棱长恰为10cm,试问蜘蛛想捉到苍蝇的最短路线是10$\sqrt{5}$cm.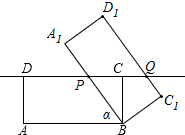 已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α<8)得到矩形A1B1C1D1.这两边所在的直线分别与CD边所在的直线相交于点P,Q,当DP:DQ=1:2时,DP的长为5.
已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α<8)得到矩形A1B1C1D1.这两边所在的直线分别与CD边所在的直线相交于点P,Q,当DP:DQ=1:2时,DP的长为5.