题目内容
4.先化简,再求值.(1)(a-2b)2+(a-b)(a+b)-2(a-3b)(a-b),其中$a=\frac{1}{2}$,b=-3.
(2)先化简,后求值:$\frac{x-1}{x+2}$•$\frac{x^2-4}{x^2-2x+1}$÷$\frac{1}{x^2-1}$,其中x2-x=0.
分析 (1)原式利用平方差公式,完全平方公式,以及多项式乘以多项式法则计算,去括号合并得到最简结果,把a与b的值代入计算即可求出值;
(2)原式利用除法法则变形,约分得到最简结果,把已知等式代入计算即可求出值.
解答 解:(1)原式=a2-4ab+4b2+a2-b2-2a2+8ab-6b2=4ab-3b2,
当a=$\frac{1}{2}$,b=-3时,原式=-33;
(2)原式=$\frac{x-1}{x+2}$•$\frac{(x+2)(x-2)}{(x-1)^{2}}$•(x+1)(x-1)=(x-2)(x+1)=x2-x-2,
当x2-x=0时,原式=0-2=-2.
点评 此题考查了分式的化简求值,以及整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
9.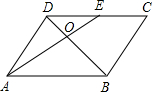 如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )
如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )
 如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )
如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )| A. | 24cm2 | B. | 36cm2 | C. | 48cm2 | D. | 60cm2 |
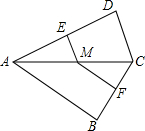 如图,四边形ABCD中,∠B=∠D=90°,M是AC上一点,ME⊥AD于点E,MF⊥BC于点F
如图,四边形ABCD中,∠B=∠D=90°,M是AC上一点,ME⊥AD于点E,MF⊥BC于点F 如图,AB为⊙O的直径,若AB⊥EF于C,试填写一个你认为正确的结论:EC=CF.
如图,AB为⊙O的直径,若AB⊥EF于C,试填写一个你认为正确的结论:EC=CF.