题目内容
19.在平面直角坐标系中,O为坐标原点,点A的坐标为(3,4),B为坐标轴上一点,且使得△AOB为等腰三角形,则满足条件的点B的个数为8.分析 分别以O、A为圆心,以OA长为半径作圆,与坐标轴交点即为所求点B,再作线段OA的垂直平分线,与坐标轴的交点也是所求的点B,作出图形,利用数形结合求解即可.
解答 解:如图,满足条件的点B的个数为8.
故答案为8.
点评 本题考查了坐标与图形的性质及等腰三角形的判定;对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.

练习册系列答案
相关题目
11.一次考试中,某题的得分情况如下表所示,则x等于30%.
| 得分(分) | 0 | 1 | 2 | 3 | 4 |
| 百分率 | 10% | 25% | x | 30% | 5% |
8.若抛物线y=x2+(m-1)x+(m+3)的顶点在坐标轴上,则m的值有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.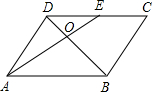 如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )
如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )
 如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )
如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )| A. | 24cm2 | B. | 36cm2 | C. | 48cm2 | D. | 60cm2 |
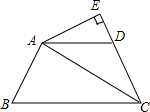 已知四边形ABCD中,AB=AD,CA平分△BCD,AE⊥CD交CD延长线于E.请问线段BC,CE及DE间有何关系?说明理由.
已知四边形ABCD中,AB=AD,CA平分△BCD,AE⊥CD交CD延长线于E.请问线段BC,CE及DE间有何关系?说明理由.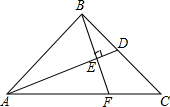 如图,在Rt△ABC中,∠ABC=90°,点D为BC边上的点,BE⊥AD于点E,延长
如图,在Rt△ABC中,∠ABC=90°,点D为BC边上的点,BE⊥AD于点E,延长 如图,锐角△ABC的外接圆O.在BC边上取两点D、E使∠BAD=∠CAE,EM⊥AB于点M,EN⊥AC于点N,AD的延长线交⊙O于点P.求证:AP•MN=AB•AC•sin∠BAC.
如图,锐角△ABC的外接圆O.在BC边上取两点D、E使∠BAD=∠CAE,EM⊥AB于点M,EN⊥AC于点N,AD的延长线交⊙O于点P.求证:AP•MN=AB•AC•sin∠BAC.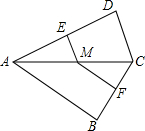 如图,四边形ABCD中,∠B=∠D=90°,M是AC上一点,ME⊥AD于点E,MF⊥BC于点F
如图,四边形ABCD中,∠B=∠D=90°,M是AC上一点,ME⊥AD于点E,MF⊥BC于点F