题目内容
已知二次函数y=x2-2(m+1)x+m2+5=0的图象过(a,0)和(b,0).
(1)若(a-1)(b-1)=28,求m的值;
(2)已知等腰△ABC一边长为7,若a、b旳值恰好是△ABC另外两边的边长,求这个三角形的周长.
(1)若(a-1)(b-1)=28,求m的值;
(2)已知等腰△ABC一边长为7,若a、b旳值恰好是△ABC另外两边的边长,求这个三角形的周长.
考点:二次函数图象上点的坐标特征,等腰三角形的性质
专题:计算题
分析:(1)根据二次函数与x轴的交点问题得到方程x2-2(m+1)x+m2+5=0的两根分别为a、b,则a+b=2(m+1),ab=m2+5,再由(a-1)(b-1)=28变形得到ab-(a+b)+1=28,则m2+5-2(m+1)+1=28,解得m1=6,m2=-4,然后根据判别式的意义确定m的值;
(2)先计算方程x2-2(m+1)x+m2+5=0的判别式,得到△=8m-16,当a=b,即△=8m+16=0,解得m=2,a+b=6,根据三角形三边的关系可判断m=2不合题意舍去;当△>0,即m>2时,把x=7代入x2-2(m+1)x+m2+5=0得m2-28m+40=0,解得m=
=14±2
,根据判别式的意义得m=14+2
,
根据根与系数的关系得a+b=2(m+1)=30+4
,于是得到这个三角形的周长=31+4
.
(2)先计算方程x2-2(m+1)x+m2+5=0的判别式,得到△=8m-16,当a=b,即△=8m+16=0,解得m=2,a+b=6,根据三角形三边的关系可判断m=2不合题意舍去;当△>0,即m>2时,把x=7代入x2-2(m+1)x+m2+5=0得m2-28m+40=0,解得m=
28±4
| ||
| 2 |
| 39 |
| 39 |
根据根与系数的关系得a+b=2(m+1)=30+4
| 39 |
| 39 |
解答:解:(1)∵二次函数y=x2-2(m+1)x+m2+5的图象过(a,0)和(b,0),
∴方程x2-2(m+1)x+m2+5=0的两根分别为a、b,
∴a+b=2(m+1),ab=m2+5,
∵(a-1)(b-1)=28,即ab-(a+b)+1=28,
∴m2+5-2(m+1)+1=28,
整理得m2-2m-24=0,解得m1=6,m2=-4,
当m=6时,x2-14x+41=0,△=142-4×41=32>0,方程有两个不相等的实数解;
当m=-4时,x2+6x+21=0,△=62-4×21<0,方程没有实数解,
∴m的值为6;
(2)x2-2(m+1)x+m2+5=0,
△=4(m+1)2-4(m2+5)=8m-16,
当a=b,即△=8m+16=0,解得m=2,
∴a+b=2(m+1)=6,
∵a+b<7,所以m=2舍去;
当△>0,即8m-16>0,m>2时,把x=7代入x2-2(m+1)x+m2+5=0得49-14(2m+1)+m2+5=0,
整理得m2-28m+40=0,
解得m=
=14±2
,
所以m=14+2
,
∴a+b=2(m+1)=30+4
,
∴这个三角形的周长=7+30+4
=31+4
.
∴方程x2-2(m+1)x+m2+5=0的两根分别为a、b,
∴a+b=2(m+1),ab=m2+5,
∵(a-1)(b-1)=28,即ab-(a+b)+1=28,
∴m2+5-2(m+1)+1=28,
整理得m2-2m-24=0,解得m1=6,m2=-4,
当m=6时,x2-14x+41=0,△=142-4×41=32>0,方程有两个不相等的实数解;
当m=-4时,x2+6x+21=0,△=62-4×21<0,方程没有实数解,
∴m的值为6;
(2)x2-2(m+1)x+m2+5=0,
△=4(m+1)2-4(m2+5)=8m-16,
当a=b,即△=8m+16=0,解得m=2,
∴a+b=2(m+1)=6,
∵a+b<7,所以m=2舍去;
当△>0,即8m-16>0,m>2时,把x=7代入x2-2(m+1)x+m2+5=0得49-14(2m+1)+m2+5=0,
整理得m2-28m+40=0,
解得m=
28±4
| ||
| 2 |
| 39 |
所以m=14+2
| 39 |
∴a+b=2(m+1)=30+4
| 39 |
∴这个三角形的周长=7+30+4
| 39 |
| 39 |
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了等腰三角形的性质和根与系数的关系.

练习册系列答案
相关题目
3点半钟时,钟表的时针与分针的夹角是( )
| A、30° | B、45° |
| C、60° | D、75° |
如图1是玩具拼图模板的一部分,已知△ABC的六个元素,则图2中甲、乙、丙三个三角形中能和△ABC完全重合的是( )
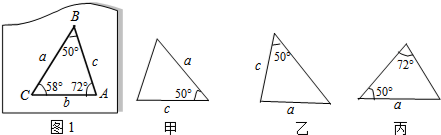
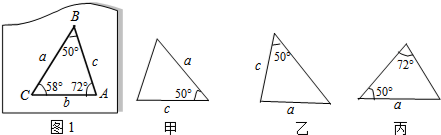
| A、甲和丙 | B、丙和乙 |
| C、只有甲 | D、只有丙 |
大于-4.2且小于3.8的整数有( )
| A、5个 | B、6个 | C、7个 | D、8个 |
 如图,直线AB与坐标轴交于A(1,0)、B(0,2)两点,过A,B两点的抛物线与x轴的另一交点为(3,0),P为抛物线上的一动点,当∠PBA=45°时,P点的坐标为
如图,直线AB与坐标轴交于A(1,0)、B(0,2)两点,过A,B两点的抛物线与x轴的另一交点为(3,0),P为抛物线上的一动点,当∠PBA=45°时,P点的坐标为 一根水平面放置的圆柱形排水管横截面如图所示,已知排水管道的直径是1米,测得OC⊥AB,垂足为C,且OC=0.3米,则水平面宽AB=
一根水平面放置的圆柱形排水管横截面如图所示,已知排水管道的直径是1米,测得OC⊥AB,垂足为C,且OC=0.3米,则水平面宽AB=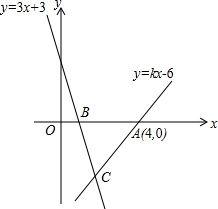 如图,直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
如图,直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.