题目内容
20．通分：$\frac{a}{{a}^{2}-1}$，$\frac{1}{{a}^{2}-4a+4}$．分析 先对两个分式的分母分别进行因式分解，然后再通分．
解答 解：∵两个分式分母分别为（a+1）（a-1）、（a-2）2，
∴最简公分母为（a+1）（a-1）（a-2）2=（a2-1）（a2-4a+4），
∴将$\frac{a}{{a}^{2}-1}$，$\frac{1}{{a}^{2}-4a+4}$通分可得：$\frac{a（a-2）^{2}}{（{a}^{2}-1）（{a}^{2}-4a+4）}$和$\frac{{a}^{2}-1}{（{a}^{2}-1）（{a}^{2}-4a+4）}$．
点评 本题考查了通分．解答此题的关键是熟知找公分母的方法：
（1）系数取各系数的最小公倍数；
（2）凡出现的因式都要取；
（3）相同因式的次数取最高次幂．
练习册系列答案
阅读快车系列答案
相关题目
如图，某校有一块长为（3a+2b）米，宽为（2a+3b）米的长方形地块，规划将阴影部分进行绿化，中间将修建一座雕像，则绿化的面积是多少平方米？并求出当a=4，b=3时的绿化面积．
天水历史悠久，文物古迹星罗棋布，是中国历史文化名城，也是中国优秀旅游城市．如图是秦州区的部分旅游景点，请你以中心广场为坐标原点建立坐标系，并写出各景点的坐标：
9．
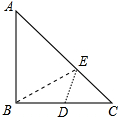如图，在Rt△ABC中，AB=BC=4，D为BC的中点，在AC边上存在一点E，连接ED，EB，则△BDE周长的最小值是（ ）
如图，在Rt△ABC中，AB=BC=4，D为BC的中点，在AC边上存在一点E，连接ED，EB，则△BDE周长的最小值是（ ）| A． | $2\sqrt{5}+2$ | B． | $2\sqrt{3}$ | C． | $2\sqrt{5}$ | D． | $2\sqrt{3}+2$ |