题目内容
 如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DEF是等腰直角三角形;②四边形CDFE可能为正方形;③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是
如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DEF是等腰直角三角形;②四边形CDFE可能为正方形;③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是考点:全等三角形的判定与性质,等腰直角三角形
专题:探究型
分析:连结CF,如图,根据等腰直角△ABC的性质得CF=AF=BF,CF⊥AB,∠1=45°,则可根据“SAS”判断△ADF≌△CEF,得到DF=EF,∠3=∠2,由∠3+∠CFD=90°可得∠3+∠2=90°,即∠DFE=90°,所以△DEF为等腰直角三角形,于是可对①进行判断;由于当FD⊥AC时,FE⊥BC,则AD=CE=
AC,此时四边形CDFE为正方形,于是可对②进行判断;利用△DEF为等腰直角三角形得到DE=
FD,利用垂线段最短,当FD⊥AC时,FD的长度最小,此时FD=
AC=4,所以DE长度的最小值为4
,则可对③进行判断;利用S△ADF=S△CEF可得四边形CDFE的面积=S△ACF=
S△ABC=16,于是可对④进行判断;由于S△CDE=S四边形CDFE-S△DEF=16-S△DEF,FD的长度的最小值为4,则S△DEF的最小值值为8,所以△CDE面积的最大值为8,则可对⑤进行判断.
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
解答:解: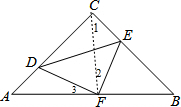 连结CF,如图,
连结CF,如图,
∵△ABC为直角三角形,
∴∠A=45°,
∵F是等腰直角△ABC斜边上的中点,
∴CF=AF=BF,CF⊥AB,∠1=45°,
在△ADF和△CEF中,
,
∴△ADF≌△CEF(SAS),
∴DF=EF,∠3=∠2,
∵∠3+∠CFD=90°,
∴∠3+∠2=90°,即∠DFE=90°,
∴△DEF为等腰直角三角形,所以①正确;
当FD⊥AC时,FE⊥BC,则AD=CE=
AC,此时四边形CDFE为正方形,所以②正确;
∵△DEF为等腰直角三角形,
∴DE=
FD,
当FD⊥AC时,FD的长度最小,此时FD=
AC=4,
∴DE长度的最小值为4
,所以③错误;
∵△ADF≌△CEF,
∴S△ADF=S△CEF,
∴四边形CDFE的面积=S△ACF=
S△ABC=
×
×8×8=16,所以④正确;
∵S△CDE=S四边形CDFE-S△DEF=16-S△DEF,
而当FD⊥AC时,FD的长度最小,此时FD=
AC=4,
∴S△DEF的最小值为
×4×4=8,
∴△CDE面积的最大值为16-8=8,所以⑤正确.
故答案为①②④⑤.
 连结CF,如图,
连结CF,如图,∵△ABC为直角三角形,
∴∠A=45°,
∵F是等腰直角△ABC斜边上的中点,
∴CF=AF=BF,CF⊥AB,∠1=45°,
在△ADF和△CEF中,
|
∴△ADF≌△CEF(SAS),
∴DF=EF,∠3=∠2,
∵∠3+∠CFD=90°,
∴∠3+∠2=90°,即∠DFE=90°,
∴△DEF为等腰直角三角形,所以①正确;
当FD⊥AC时,FE⊥BC,则AD=CE=
| 1 |
| 2 |
∵△DEF为等腰直角三角形,
∴DE=
| 2 |
当FD⊥AC时,FD的长度最小,此时FD=
| 1 |
| 2 |
∴DE长度的最小值为4
| 2 |
∵△ADF≌△CEF,
∴S△ADF=S△CEF,
∴四边形CDFE的面积=S△ACF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S△CDE=S四边形CDFE-S△DEF=16-S△DEF,
而当FD⊥AC时,FD的长度最小,此时FD=
| 1 |
| 2 |
∴S△DEF的最小值为
| 1 |
| 2 |
∴△CDE面积的最大值为16-8=8,所以⑤正确.
故答案为①②④⑤.
点评:本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.也考查了等腰直角三角形的判断与性质和三角形面积公式.

练习册系列答案
相关题目
要使式子-
有意义,字母x的取值必须满足( )
| ||
| x-3 |
A、x≤
| ||
B、x≥-
| ||
C、x≥
| ||
D、x≥
|
 如图,点D为等边三角形ABC外一点,BD=DA,BE=BA,∠DBE=∠DBC,则∠E的度数是( )
如图,点D为等边三角形ABC外一点,BD=DA,BE=BA,∠DBE=∠DBC,则∠E的度数是( )| A、10° | B、20° |
| C、30° | D、40° |
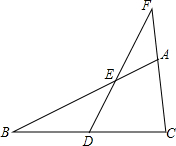 已知:如图,在△ABC中,点D是BC的中点,过点D作直线交AB,CA的延长线于点E,F.当BE=CF时,求证:AE=AF.
已知:如图,在△ABC中,点D是BC的中点,过点D作直线交AB,CA的延长线于点E,F.当BE=CF时,求证:AE=AF. 如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C(直线l不与线段AB相交),过A、B两点分别作直线l的垂线AE、BF,E、F为垂足.
如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C(直线l不与线段AB相交),过A、B两点分别作直线l的垂线AE、BF,E、F为垂足. 如图,在△ABC中,AB=AC,D是BC上一点,过点D作DE∥AB,且使DE=AC,连接AD,AE,EC.
如图,在△ABC中,AB=AC,D是BC上一点,过点D作DE∥AB,且使DE=AC,连接AD,AE,EC. 如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一条直线上,且AB=,BC=1,AG分别交DC,DE,FE于点P,Q,R.
如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一条直线上,且AB=,BC=1,AG分别交DC,DE,FE于点P,Q,R. 如图,△ABC绕点A旋转到△ADE处,且B、C、D在同一直线上,若∠B=40°,则∠CDE=
如图,△ABC绕点A旋转到△ADE处,且B、C、D在同一直线上,若∠B=40°,则∠CDE=