题目内容
 如图,点D为等边三角形ABC外一点,BD=DA,BE=BA,∠DBE=∠DBC,则∠E的度数是( )
如图,点D为等边三角形ABC外一点,BD=DA,BE=BA,∠DBE=∠DBC,则∠E的度数是( )| A、10° | B、20° |
| C、30° | D、40° |
考点:全等三角形的判定与性质,等腰三角形的性质,等边三角形的性质
专题:
分析:利用等边三角形的性质得出BE=BC,再利用“SAS”得出△EBD≌△CBD,进而结合等腰三角形的性质得出∠BCD的度数即可得出答案.
解答: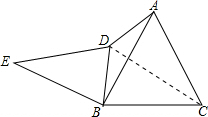 解:连接DC,
解:连接DC,
∵△ABC是等边三角形,
∴AB=BC=AC,
∵BE=AB,
∴BE=BC,
在△EBD和△CBD中,
,
∴△EBD≌△CBD(SAS),
∠E=∠BCD,
∵BD=AD,BC=AC,
∴DC⊥AB,则∠BCD=∠ACD=30°,
∴∠E=30°.
故选:C.
 解:连接DC,
解:连接DC,∵△ABC是等边三角形,
∴AB=BC=AC,
∵BE=AB,
∴BE=BC,
在△EBD和△CBD中,
|
∴△EBD≌△CBD(SAS),
∠E=∠BCD,
∵BD=AD,BC=AC,
∴DC⊥AB,则∠BCD=∠ACD=30°,
∴∠E=30°.
故选:C.
点评:此题主要考查了全等三角形的判定与性质以及等边三角形的性质,得出△EBD≌△CBD是解题关键.

练习册系列答案
相关题目
关于x的分式方程2k-4+
=
仅有一个实数根,则实数k的取值共有( )
| k+1 |
| x |
| k-5 |
| x+2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列调查方式,你认为最合适的是( )
| A、日光灯管厂要检测一批灯管的使用寿命,采用普查方式 |
| B、了解海门市每天的流动人口数,采用抽样调查方式 |
| C、了解海门市民对各类电视节目的喜爱情况,采用普查方式 |
| D、旅客上飞机前的安检,采用抽样调查方式 |
 如图已知,CE⊥AB,BF⊥AC,BF交CE于点D,且BD=CD.
如图已知,CE⊥AB,BF⊥AC,BF交CE于点D,且BD=CD. 如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DEF是等腰直角三角形;②四边形CDFE可能为正方形;③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是
如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DEF是等腰直角三角形;②四边形CDFE可能为正方形;③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是 已知:如图,点A,B,C,D在一条直线上,AB=CD,AE∥FD,且∠E=∠F.求证:EC=FB.
已知:如图,点A,B,C,D在一条直线上,AB=CD,AE∥FD,且∠E=∠F.求证:EC=FB. 如图,梯形ABCD中,AB∥CD,∠BCD=90°,CD=8,AD=13.将该梯形沿BD翻折,使点C恰好与边AD上点E重合,那么BC=
如图,梯形ABCD中,AB∥CD,∠BCD=90°,CD=8,AD=13.将该梯形沿BD翻折,使点C恰好与边AD上点E重合,那么BC=