题目内容
9.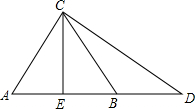 已知:如图,等边△ABC,延长AB到D,使BD=AB.又CE是AB边上中线.求证:CE=$\frac{1}{2}$CD.
已知:如图,等边△ABC,延长AB到D,使BD=AB.又CE是AB边上中线.求证:CE=$\frac{1}{2}$CD.
分析 由△ABC是等边三角形,得到∠ABC=60°,AB=BC=AC,等量代换得到BC=BD,根据外角的性质得到∠D=∠DCB=$\frac{1}{2}∠$ABC=30°,根据等腰三角形的性质得到CE⊥AB,即可得到结论.
解答 证明:∵△ABC是等边三角形,
∴∠ABC=60°,AB=BC=AC,
∵BD=AB,
∴BC=BD,
∴∠D=∠DCB=$\frac{1}{2}∠$ABC=30°,
∵CE是AB边上中线,
∴CE⊥AB,
∴CE=$\frac{1}{2}$CD.
点评 本题考查了含30°角的直角三角形的性质,等边三角形的性质,熟练掌握含30°角的直角三角形的性质是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
19. 如图,△ABC≌△EFD,AB=EF,AE=15,CD=3,则AC=( )
如图,△ABC≌△EFD,AB=EF,AE=15,CD=3,则AC=( )
 如图,△ABC≌△EFD,AB=EF,AE=15,CD=3,则AC=( )
如图,△ABC≌△EFD,AB=EF,AE=15,CD=3,则AC=( )| A. | 5 | B. | 6 | C. | 9 | D. | 12 |
 如图,在⊙O中,$\widehat{AC}$=$\widehat{BD}$,∠1=35°,求∠2的度数.
如图,在⊙O中,$\widehat{AC}$=$\widehat{BD}$,∠1=35°,求∠2的度数.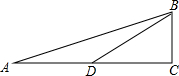 已知,如图,在Rt△ABC中,∠BCA=90°,∠A=15°,D是AC边上一点,BC=$\frac{1}{2}$BD.求证:点D在AB的垂直平分线上.
已知,如图,在Rt△ABC中,∠BCA=90°,∠A=15°,D是AC边上一点,BC=$\frac{1}{2}$BD.求证:点D在AB的垂直平分线上. 如图是由5个大小相同的正方体组合而成的几何体,它的主视图是( )
如图是由5个大小相同的正方体组合而成的几何体,它的主视图是( )


