题目内容
17．
如图，在⊙O中，$\widehat{AC}$=$\widehat{BD}$，∠1=35°，求∠2的度数．
分析 由$\widehat{AC}$=$\widehat{BD}$易得$\widehat{CD}$=$\widehat{AB}$，然后根据圆心角、弧、弦的关系得到∠2=∠1=35°．
解答 解：∵$\widehat{AC}$=$\widehat{BD}$，
∴$\widehat{CD}$+$\widehat{BC}$=$\widehat{BC}$+$\widehat{AB}$，
∴$\widehat{CD}$=$\widehat{AB}$，
∴∠2=∠1=35°．
点评 本题考查了圆心角、弧、弦的关系：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．
练习册系列答案
相关题目
8．绝对值小于2015的所有整数的乘积为（ ）
| A． | 2015 | B． | 1 | C． | 0 | D． | -2015 |
12．下表是2015年6月份的月历表，任意圈出一横行或一竖列相邻的三个数，则这三个数的和不可能是（ ）
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 |
| A． | 24 | B． | 43 | C． | 57 | D． | 69 |
2．已知二次函数y=ax2+bx+c，函数y与自变量x的部分对应值如下表：
则当y＞-1时，x的取值范围是-2＜x＜2．
| x | … | -4 | -2 | 0 | 2 | 4 | … |
| y | … | -4 | -1 | 0 | -1 | -4 | … |
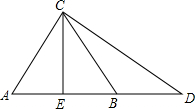已知：如图，等边△ABC，延长AB到D，使BD=AB．又CE是AB边上中线．求证：CE=$\frac{1}{2}$CD．