题目内容
如图,已知平行四边形ABCD中,AB=5,BC=8,cosB= ,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )
,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )
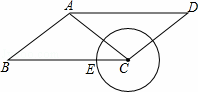
A. 0<CE≤8 B. 0<CE≤5
C. 0<CE<3或5<CE≤8 D. 3<CE≤5
C
考点: 直线与圆的位置关系;平行四边形的性质.
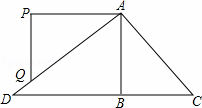
分析: 过A作AM⊥BC于N,CN⊥AD于N,根据平行四边形的性质求出AD∥BC,AB=CD=5,求出AM、CN、AC、CD的长,即可得出符合条件的两种情况.
解答: 解: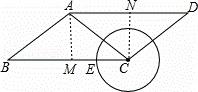
过A作AM⊥BC于N,CN⊥AD于N,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=5,
∴AM=CN,
∵AB=5,cosB=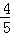 =
=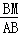 ,
,
∴BM=4,
∵BC=8,
∴CM=4=BC,
∵AM⊥BC,
∴AC=AB=5,
由勾股定理得:AM=CN=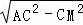 =3,
=3,
∴当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是0<CE<3或5<CE≤8,
故选C.
点评: 本题考查了直线和圆的位置关系,勾股定理,平行四边形的性质的应用,能求出符合条件的所有情况是解此题的关键,此题综合性比较强,有一定的难度.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 )÷(﹣1
)÷(﹣1 )+(﹣2)2×(﹣3)
)+(﹣2)2×(﹣3)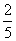 B.
B.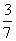 C.
C.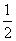 D.
D.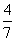
 单位,得到抛物线Q′和平行四边形O′A′C′B′,在向下平移的过程中,设平行四边形O′A′C′B′与平
单位,得到抛物线Q′和平行四边形O′A′C′B′,在向下平移的过程中,设平行四边形O′A′C′B′与平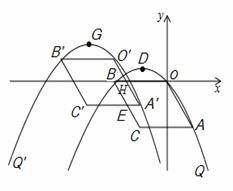
 于点O,OE平分∠COB,若∠EOB=55
于点O,OE平分∠COB,若∠EOB=55
