题目内容
9.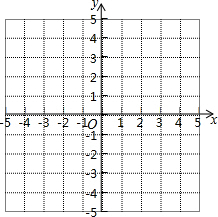 已知:一次函数y=2x+4
已知:一次函数y=2x+4(1)在如图所示的平面直角坐标系中,画出函数的图象;
(2)若图象与x轴的交点为A,与y轴交点为B,求出△AOB的面积;
(3)利用图象直接写出:当y<0时,x的取值范围.
分析 (1)过图象上两个点的坐标画出直线即可;
(2)求出A、B的坐标,根据三角形的面积公式求出即可;
(3)根据A点的坐标结合图象得出即可.
解答 解:(1)如图所示: ;
;
(2)∵A(-2,0),B(0,4),
∴AO=2,BO=4,
∴S△ABO=$\frac{1}{2}×OA×OB$=$\frac{1}{2}×2×4$=4;
(3)由图象知,当x<-2时,y<0.
点评 本题考查了一次函数图象上点的坐标特征,一次函数的图象和性质等知识点,能熟记一次函数函数图象和性质的内容是解此题的关键,注意数形结合思想的运用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
9.为了解中考体育科目训练情况,某校从九年级学生中随机抽取部分学生进行了一次中考体育科目测试(把测试结果分为A,B,C,D四个等级),并将测试结果绘制成了如图所示的两幅不完整统计图,根据统计图中提供的信息,结论错误的是( )


| A. | 本次抽样测试的学生人数是40 | |
| B. | 在图1中,∠α的度数是126° | |
| C. | 该校九年级有学生500名,估计D级的人数为80 | |
| D. | 从被测学生中随机抽取一位,则这位学生的成绩是A级的概率为0.2 |
6.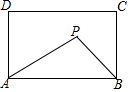 如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=$\frac{1}{3}$S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为( )
如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=$\frac{1}{3}$S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为( )
 如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=$\frac{1}{3}$S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为( )
如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=$\frac{1}{3}$S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为( )| A. | $\sqrt{29}$ | B. | $\sqrt{34}$ | C. | 5$\sqrt{2}$ | D. | $\sqrt{41}$ |
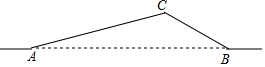 如图,从A地到B地的公路需经过C地,图中AC=6千米,∠CAB=15°,∠CBA=30°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=6千米,∠CAB=15°,∠CBA=30°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
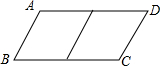 邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图,?ABCD中,若AB=1,BC=2,则□ABCD为1阶准菱形.
邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图,?ABCD中,若AB=1,BC=2,则□ABCD为1阶准菱形.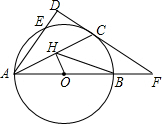 如图,AB是⊙O的直径,C为⊙O上一点,AD与过C点的切线垂直,垂足为D,AD交⊙O于E,DE=2,CD=4.
如图,AB是⊙O的直径,C为⊙O上一点,AD与过C点的切线垂直,垂足为D,AD交⊙O于E,DE=2,CD=4.