题目内容
16.化简.(不取近似值)(1)$\sqrt{3+2\sqrt{2}}$;
(2)$\sqrt{4-2\sqrt{3}}$.
分析 (1)根据完全平方公式,可得二次根式的性质,再根据二次根式的性质,可得答案;
(2)根据完全平方公式,可得二次根式的性质,再根据二次根式的性质,可得答案.
解答 解:(1)原式=$\sqrt{(\sqrt{2})^{2}+2\sqrt{2}+1}$=$\sqrt{(\sqrt{2}+1)^{2}}$=$\sqrt{2}$+1;
(2)原式=$\sqrt{(\sqrt{3})^{2}-2\sqrt{3}+1}$=$\sqrt{(\sqrt{3}-1)^{2}}$=$\sqrt{3}$-1.
点评 本题考查了二次根式的性质与化简,利用完全平方公式得出被开方数是平方的形式是解题关键,又利用了二次根式的性质.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
7.由于被墨水污染,一道数学题仅能见到如下文字:“已知二次函数y=x2+bx+c的图象过点(1,0)…求证:这个二次函数的图象关于直线x=2对称.”根据现有信息,题中的二次函数图象不具有的性质是( )
| A. | 过点(3,0) | B. | 顶点是(2,-2) | C. | b<0 | D. | c=3 |
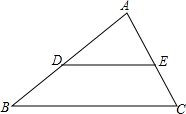 如图,$\frac{BD}{AB}=\frac{CE}{AC}$,BC=20,CE:EA=2:3,求DE的长.
如图,$\frac{BD}{AB}=\frac{CE}{AC}$,BC=20,CE:EA=2:3,求DE的长.