题目内容
5．已知$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{4}$=$\frac{d}{5}$，求$\frac{2a+3b}{4c+5d}$的值．（提示：用设k法来解题）分析 根据比的意义，可用k表示a，用k表示b，用k表示c，用k表示d，再根据分式的性质，可得答案．
解答 解：设知$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{4}$=$\frac{d}{5}$=k，
a=2k，b=3k，c=4k，d=5k．
$\frac{2a+3b}{4c+5d}$=$\frac{2×2k+3×3k}{4×4k+5×5k}$=$\frac{13}{41}$．
点评 本题考查了比例的性质，利用比的意义得出a=2k，b=3k，c=4k，d=5k是解题关键，又利用了分式的性质．
练习册系列答案
字词句篇与同步作文达标系列答案
走进文言文系列答案
相关题目
15．
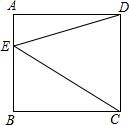如图，在正方形ABCD中．E是AB上的三分之一点．连结DE、CE，则S△BCE：S正方形ABCD等于（ ）
如图，在正方形ABCD中．E是AB上的三分之一点．连结DE、CE，则S△BCE：S正方形ABCD等于（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |
13．2012年全年国内生产总值519000亿元，用科学记数法表示（ ）亿元．
| A． | 0.519×106 | B． | 5.19×105 | C． | 5.19×106 | D． | 0.519×105 |
