题目内容
1.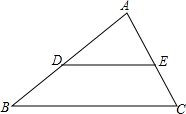 如图,$\frac{BD}{AB}=\frac{CE}{AC}$,BC=20,CE:EA=2:3,求DE的长.
如图,$\frac{BD}{AB}=\frac{CE}{AC}$,BC=20,CE:EA=2:3,求DE的长.
分析 根据$\frac{BD}{AB}=\frac{CE}{AC}$,得到$\frac{AD}{AB}=\frac{AE}{AC}$,又∠A=∠A,可证△ADE∽△ABC,根据相似三角形对应边成比例求出DE的长即可.
解答 解:∵$\frac{BD}{AB}=\frac{CE}{AC}$,
∴$\frac{AD}{AB}=\frac{AE}{AC}$,
又∵∠A=∠A,
∴△ADE∽△ABC,
∴$\frac{AE}{AC}=\frac{DE}{BC}$,
∵CE:EA=2:3,
∴AE:AC=3:5,
∴DE:20=3:5,
∴DE=12.
点评 本题考查了相似三角形的判定与性质,证明△ADE∽△ABC是解决问题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
13.2012年全年国内生产总值519000亿元,用科学记数法表示( )亿元.
| A. | 0.519×106 | B. | 5.19×105 | C. | 5.19×106 | D. | 0.519×105 |
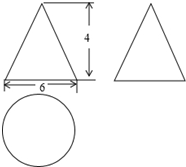 已知一个几何体的三视图如图所示,
已知一个几何体的三视图如图所示, 画出下图四棱柱的主视图、左视图和俯视图.
画出下图四棱柱的主视图、左视图和俯视图.