题目内容
11.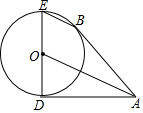 如图,AB,AD为⊙O的切线,切点分别为B,D,DE为⊙O的直径,连接BE,OA
如图,AB,AD为⊙O的切线,切点分别为B,D,DE为⊙O的直径,连接BE,OA(1)求证:BE∥OA;
(2)若AD=DE,求sin∠DAB的值.
分析 (1)连接OD,证Rt△ABO≌Rt△ADO,则∠AOD=∠AOB,又∠DOB是等腰△OBE的外角,则∠DOB=2∠EBO,由此可证得∠EBO=∠AOB,内错角相等,则BE∥OA;
(2)由已知求得∠OAD的正余弦三角函数值,根据倍角正弦公式即可求得结论.
解答  (1)证明:连接OB,
(1)证明:连接OB,
∵AB,AD为⊙O的切线,
∴∠ABO=∠ADO=90°.
∵OD=OB,
在Rt△ABO和Rt△ADO中
$\left\{\begin{array}{l}{OA=OA}\\{OB=OD}\end{array}\right.$
∴Rt△ABO≌Rt△ADO,
∴∠AOD=∠AOB,
又∵OE=OB,
∴∠E=∠EBO,
∵∠E=$\frac{1}{2}$∠BOD=∠AOB,
∴∠EBO=∠AOB,
∴BE∥OA;
(2)∵AD=DE,
∴AD=2OD,
∴sin∠DAO=$\frac{\sqrt{5}}{5}$,cos∠DAO=$\frac{2\sqrt{5}}{5}$,
∴sin∠DAB=sin2∠DAO=2sin∠DAOcos∠DAO=2×$\frac{\sqrt{5}}{5}$×$\frac{2\sqrt{5}}{5}$=$\frac{4}{5}$.
点评 此题主要考查了切线的性质、平行线的判定、全等三角形的判定和性质,正余弦函数,倍角公式等知识,熟练掌握切线的性质是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目

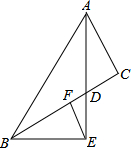 如图,△ABC中,AD是角平分线,BE⊥AD,垂足E在AD延长线上,F是BC的中点,AB=30cm,AC=18cm.则EF的长为6cm.
如图,△ABC中,AD是角平分线,BE⊥AD,垂足E在AD延长线上,F是BC的中点,AB=30cm,AC=18cm.则EF的长为6cm. 如图,在四边形ABCD中,对角线AC⊥BD且AC=6,BD=8,点E、F、G分别是边AB、CD、AD的中点,则EF=5.
如图,在四边形ABCD中,对角线AC⊥BD且AC=6,BD=8,点E、F、G分别是边AB、CD、AD的中点,则EF=5.