题目内容
10.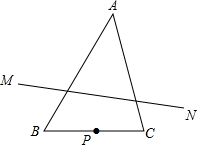 如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是2$\sqrt{6}$≤MN<4$\sqrt{2}$.
如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是2$\sqrt{6}$≤MN<4$\sqrt{2}$.
分析 连接AM、AN、AP,过点A作AD⊥MN于点D,由对称性可知AM=AP=AN、△MAN等腰直角三角形,进而即可得出MN=$\sqrt{2}$AP,再根据AP的取值范围即可得出线段MN长的取值范围.
解答 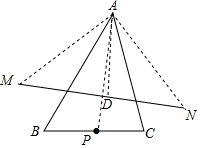 解:连接AM、AN、AP,过点A作AD⊥MN于点D,如图所示.
解:连接AM、AN、AP,过点A作AD⊥MN于点D,如图所示.
∵点P关于直线AB,AC的对称点分别为M,N,
∴AM=AP=AN,∠MAB=∠PAB,∠NAC=∠PAC,
∴△MAN等腰直角三角形,
∴∠AMD=45°,
∴AD=MD=$\frac{\sqrt{2}}{2}$AM,MN=$\sqrt{2}$AM.
∵AB=4,∠B=60°,
∴2$\sqrt{3}$≤AP≤4,
∵AM=AP,
∴2$\sqrt{6}$≤MN≤4$\sqrt{2}$.
故答案为:2$\sqrt{6}$≤MN<4$\sqrt{2}$.
点评 本题考查了轴对称的性质,等腰直角三角形的判定和性质,解题的关键是证得△AMN是等腰直角三角形.

练习册系列答案
相关题目
1.化简(x3)2的结果是( )
| A. | 2x3 | B. | x5 | C. | x6 | D. | x9 |
15. 如图,直线y=x+1与y轴交于点A1,依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、…,An在直线x+1上,点C1、C2、…,Cn在x轴上,则点Bn的坐标是( )
如图,直线y=x+1与y轴交于点A1,依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、…,An在直线x+1上,点C1、C2、…,Cn在x轴上,则点Bn的坐标是( )
 如图,直线y=x+1与y轴交于点A1,依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、…,An在直线x+1上,点C1、C2、…,Cn在x轴上,则点Bn的坐标是( )
如图,直线y=x+1与y轴交于点A1,依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、…,An在直线x+1上,点C1、C2、…,Cn在x轴上,则点Bn的坐标是( )| A. | (2n-1,2n-1) | B. | (2n-1+1,2n-1) | C. | (2n-1,2n-1) | D. | (2n-1,n) |
19.下列运算正确的是( )
| A. | (-2x2y)3=8x6y3 | B. | a6+a3=a9 | C. | (a+b)2=a2+b2 | D. | x7÷x2=x5 |
20.如果a与8互为相反数,那么a是( )
| A. | $\frac{1}{8}$ | B. | -$\frac{1}{8}$ | C. | 8 | D. | -8 |
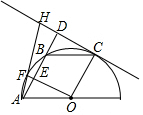 如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作CD∥OF交AB的延长线于点D,延长AF交直线CD于点H.
如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作CD∥OF交AB的延长线于点D,延长AF交直线CD于点H.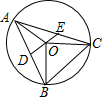 如图,△ABC内接于⊙O,OC⊥OB,OD⊥AB于D交AC于E点,已知⊙O的半径为1,则AE2+CE2的值为( )
如图,△ABC内接于⊙O,OC⊥OB,OD⊥AB于D交AC于E点,已知⊙O的半径为1,则AE2+CE2的值为( )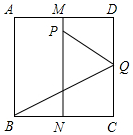 如图,面积为1的正方形ABCD中,M,N分别为AD、BC的中点,将C点折至MN上,落在P点的位置,折痕为BQ,连接PQ.以PQ为边长的正方形的面积等于$\frac{1}{3}$.
如图,面积为1的正方形ABCD中,M,N分别为AD、BC的中点,将C点折至MN上,落在P点的位置,折痕为BQ,连接PQ.以PQ为边长的正方形的面积等于$\frac{1}{3}$.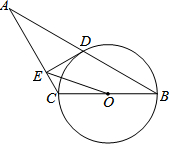 如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,DE是⊙O的切线,连结OD,OE
如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,DE是⊙O的切线,连结OD,OE