题目内容
2.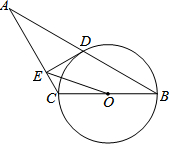 如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,DE是⊙O的切线,连结OD,OE
如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,DE是⊙O的切线,连结OD,OE(1)求证:∠DEA=90°;
(2)若BC=4,写出求△OEC的面积的思路.
分析 (1)连接OD,求出∠A=∠ODB,推出OD∥AC,即可得出答案;
(2)求出AD、CD,由Rt△AED中,∠A=30°,AD的长,得ED,AE进而求得EC由DE,AE的长得△DEC的面积由 OD∥AC,△DEC的面积和△OEC的面积相等,即可得出△OEC的面积.
解答 (1)证明:连结OD,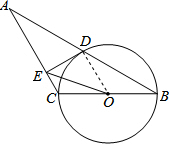
∵△ABC 是等腰三角形,
∴CA=CB,
∴∠A=∠B,
又∵OD=OB,
∴∠ODB=∠B,
∴∠A=∠ODB,
∴OD∥AC,
∵DE是⊙O的切线,
∴OD⊥DE,
∴AC⊥DE,
∴∠DE A=90°;
(2)解:连结CD,
由BC是直径,得∠CDB=∠CDA=90°,
∵由 Rt△CDA中,BC=AC=4,∠A=30°,
∴CD=$\frac{1}{2}$AB=2,AD=$\sqrt{3}$CD=2$\sqrt{3}$,
∵由Rt△AED中,∠A=30°,
∴DE=$\frac{1}{2}$AD=$\sqrt{3}$,AE=$\sqrt{3}$DE=3,
EC=AC-AE=1,
∴△EDC的面积=$\frac{1}{2}×DE×EC$=$\frac{1}{2}×1×\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
∵OD∥AC,
∴△DEC的面积和△OEC的面积相等,
∴△OEC的面积是$\frac{\sqrt{3}}{2}$.
点评 本题考查了切线的性质,解直角三角形,平行线的性质和判定等知识点,能综合运用知识点进行推理和计算是解此题的关键.

练习册系列答案
相关题目
12.若抛物线y=x2-2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位,再沿铅直方向向上平移三个单位,则原抛物线图象的解析式应变为( )
| A. | y=(x-2)2+3 | B. | y=x2-1 | C. | y=(x-2)2+5 | D. | y=x2+4 |
13.下面各数中,最小的数是( )
| A. | 0 | B. | 0.01 | C. | -0.1 | D. | -1 |
17. 如图,在矩形ABCD中,AB=$\sqrt{2}$,AD=2,以点A为圆心,AD的长为半径的圆交BC边于点E,则图中阴影部分的面积为( )
如图,在矩形ABCD中,AB=$\sqrt{2}$,AD=2,以点A为圆心,AD的长为半径的圆交BC边于点E,则图中阴影部分的面积为( )
 如图,在矩形ABCD中,AB=$\sqrt{2}$,AD=2,以点A为圆心,AD的长为半径的圆交BC边于点E,则图中阴影部分的面积为( )
如图,在矩形ABCD中,AB=$\sqrt{2}$,AD=2,以点A为圆心,AD的长为半径的圆交BC边于点E,则图中阴影部分的面积为( )| A. | $2\sqrt{2}-1-\frac{π}{3}$ | B. | $2\sqrt{2}-1-\frac{π}{2}$ | C. | $2\sqrt{2}-2-\frac{π}{2}$ | D. | $2\sqrt{2}-1-\frac{π}{4}$ |
7.2015年10月成立的无锡市新吴区总面积220平方公里,常住人口约55万人,下辖6个街道;2016年末,新吴区实现地区生产总值约1302亿元,用科学记数法表示该地区生产总值应记为( )
| A. | 1302×108 | B. | 1.302×103 | C. | 1.302×1010 | D. | 1.302×1011 |
14.据西安晚报相关报道,西安市入围全国十大热门旅游城市,清明小长假期间旅游总收入9.93亿元,其中9.93亿用科学记数法表示为( )
| A. | 9.93×108 | B. | 9.93×109 | C. | 99.3×109 | D. | 9.93×107 |
11.在实数-$\sqrt{2}$,0,-1.5,1中,最小的数是( )
| A. | -$\sqrt{2}$ | B. | 0 | C. | -1.5 | D. | 1 |
12.一个正方形的面积为17,估计它的边长大小在( )
| A. | 5和6之间 | B. | 4和5之间 | C. | 3和4之间 | D. | 2和3之间 |
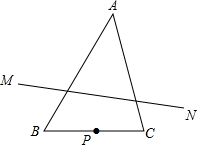 如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是2$\sqrt{6}$≤MN<4$\sqrt{2}$.
如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是2$\sqrt{6}$≤MN<4$\sqrt{2}$.