题目内容
14．
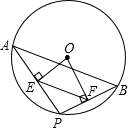如图，点A、B是⊙O上两点，AB=10，点P是⊙O上的动点（P与A、B不重合），连结AP、PB，过点O分别作OE⊥AP于点E，OF⊥AP于点E，OF⊥PB于点F，则EF=（ ）| A． | 4 | B． | 5 | C． | 5.5 | D． | 6 |
分析 先根据垂径定理得出AE=PE，PF=BF，故可得出EF是△APB的中位线，再根据中位线定理即可得出EF∥AB，EF=$\frac{1}{2}$AB即可．
解答 解：∵OE⊥AP于E，OF⊥PB于F，
∴AE=PE，PF=BF，
∴EF是△APB的中位线，
∴EF∥AB，EF=$\frac{1}{2}$AB=5；
故选B．
点评 本题考查的是垂径定理和三角形中位线定理，熟知垂直于弦的直径平分弦是解答此题的关键．
练习册系列答案
相关题目
如图所示，课间操时，小华、小军、小刚的位置如图，小华对小刚说：“如果我的位置用（0，0）表示，小军的位置用（2，1）表示，那么你的位置应表示为（4，3）．”
3．
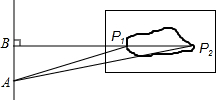如图是一跳远运动员跳远时落在沙坑的痕迹，则表示该运动员成绩的是（ ）
如图是一跳远运动员跳远时落在沙坑的痕迹，则表示该运动员成绩的是（ ）| A． | 线段AP1的长度 | B． | 线段AP2的长度 | C． | 线段BP2的长度 | D． | 线段BP1的长度 |
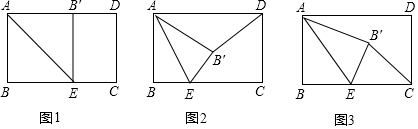
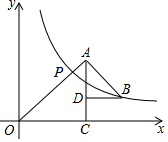如图所示，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B，与OA交于点P，且OA2-AB2=18，则点P的横坐标为（ ）
如图，已知抛物线y=-x2+9的顶点为A，曲线DE是双曲线y=$\frac{k}{x}$（3≤x≤12）的一部分，记作G1，且D（3，m）、E（12，m-3），将抛物线y=-x2+9水平向右移动a个单位，得到抛物线G2．