题目内容
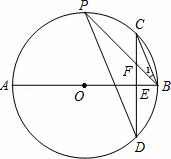
如图,B,C,D是半径为6的⊙O上的三点,已知 的长为2π,且OD∥BC,则BD的长为( )
的长为2π,且OD∥BC,则BD的长为( )

A. 3 B.6 C.6
B.6 C.6 D. 12
D. 12
C 解:连结OC交BD于E,如图,
设∠BOC=n°,
根据题意得2π= ,得n=60,即∠BOC=60°,
,得n=60,即∠BOC=60°,
而OB=OC,
∴△OBC为等边三角形,
∴∠C=60°,∠OBC=60°,BC=OB=6,
∵BC∥OD,
∴∠2=∠C=60°,
∵∠1= ∠2(圆周角定理),
∠2(圆周角定理),
∴∠1=30°,
∴BD平分∠OBC,BD⊥OC ,
,
∴BE=DE,
在Rt△CBE中,CE= BC=3,
BC=3,
∴BE= CE=3
CE=3 ,
,
∴BD=2BE=6 .
.
故选:C.


练习册系列答案
相关题目

 ,则EC的长是( )
,则EC的长是( )
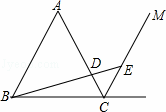

 cm,∠BCD=22°30′,则⊙O的半径为 cm.
cm,∠BCD=22°30′,则⊙O的半径为 cm.